レオナルドの時代の数学と黄金比
レオナルドの生きたルネッサンスの時代で、数学は如何なる状況にあったか。現在では数学の最先端は殆ど一般の人々には理解できないレベルに達しているが、当時はまだまだ現在の一般の人にも理解可能なレベルであったと言えよう。
数学の歴史の詳細については他書(上垣 渉著「はじめて読む数学の歴史」べレ出版、 ボイヤー著、加賀美鐡雄・浦野由有訳「数学の歴史 3」)に譲るとして、レオナルドの時代までのそれを概観する。
数学はメソポタミア、エジプトに端を発し、ヘレニズム文明に受けつがれ、ギリシャ時代に大きく進歩した。その後、中世後期レオナルドの生きた時代まで大きな進歩は無く、更なる学問的進展はガリレオ、ニュートンらの登場を待たなくてはならない。
その後人類はこの分野で爆発的進展を見せたと言ってよいであろう。現在においては、数学の最先端は到底一般人の理解出来るところではない。
レオナルドの生誕の次の年1453年コンスタンチノープルがイスラム軍の攻撃によって陥落した。この出来事は、古代ギリシャの書物が亡命者達によってイタリア等に伝わったが故に、西ヨーロッパ世界は古代の遺産に接するようになったと言われるとともに、西欧世界は文学と数学両方の古典の写本の頼りになる供給源を失ったということでもあった(ボイヤー著、加賀美鐡雄・浦野由有訳「数学の歴史 3」p1)。
それ以前の1447年に西欧で初めて本が印刷された。しかし、ギリシャ幾何学の古典を出版する必要がでるほど、数学的素養のある者は殆どいなかった。
無理数は既に紀元前400年のギリシャ時代に知られたが、一般生活においての必要性は殆ど無かったと言ってよいであろう。その記号法はまだ現在のように簡便なものは採用されていなかった。すなわち、それらの表現はレオナルドの時代以降、代数学が発展し、記号法が整備される 16世紀以降である(‘数学はじめて物語’p18)。今日のような「√」の表現が使われるようになるのはデカルト(1596~1650)後である(上垣渉著「数学の歴史」p229)。
当時は、地中海貿易の時代で、交易品の備蓄・売買・清算に必要な効率的な数値表現が求められた。現在において広く用いられている10進法、位取りの技法が広まり始めていた時代である。
フィボナッチと呼ばれる13世紀の数学者レオナルド・ダ・ピサーノが、アラビア数学をイタリアに導入して以来、ヨーロッパで最も進歩していた数学を背景にして、フィリッポ・ブルネレスキ、レオン・バティスタ・アルベルティ、ピエロ・デラ・フランチェスカらが幾何学を使って三次元空間を絵画面に再現する視点を獲得していった。
これらの識者、芸術家によって研究された幾何学は、常に二つの問題と密接に関連していた。一つは「古典古代の復興」という彼らの課題、ウィトルウィウスに基づく人体比例の問題であり、もう一つが近代科学に向う「自然を映す鏡」として視空間の斉一性を目指して線遠近法の問題だった。これらの問題はレオナルドの≪人体権衡図≫に代表されるように、共に比例関係をいかに決定するかという具体的な幾何学の問題であったと言える。
レオナルドは自然探究に希求心を強く持ち、観察眼に優れていた。それは数学領域にも及び、当時の優れた数学者であるルカ・パチョーリと、ミラノ公ルドヴィーコ・イル・モロの宮廷において知己となった。 ルカ・パチョーリ(1445~1517)は聖フランチェスコ修道士で、この時期の数学についてまとめた著作『数学大全』『神聖な比例』で名を残している。特に後者においての目的の一つは芸術の数学的基礎を完成させることであったと言える。
ピエロ・デラ・フランチェスカ(1412~1492)は現代においては画家としての方が有名であるが、この時代において数学における優れた業績を残した。パチョーリは著書『算術・幾何学・比例と比例関係大全』にピエロの成果を採り入れた。
レオナルドは当時の最先端数学の知識をパチョーリから得た。また逆にパチョーリの著書『神聖な比例』においてイラストレーターとして協力し、多くの立体の絵を描いた。 このような交友を通して、レオナルドは数学の知識を自己のものとし、絵画にその美を高めるために、数学を有効に活用する術を探究した。しかし、レオナルドは数学の分野ではとくに傑出した業績を残したとは言えないかも知れない(ボイヤー著、加賀美鐡雄・浦野由有訳「数学の歴史 3」p17)。しかし、1998年にイーレとシュレーアはレオナルドが円周率を一万分の一の精度まで計算(発見)していたことを論文で明らかにしている。
●黄金比
図1-1において線分ABを AB:AC = AC:CB となるような点Cで分割することを「黄金分割」と言い、この比 1:(1+√5)/2 のことを「黄金比」と言う。またこの比で分けることを黄金分割と言う。
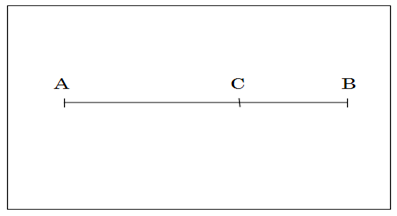
この数の表現法は勿論現代的なそれであって、この「黄金比」そのものはギリシャ時代から定義されているものである。すなわち、ユークリッドの『言論』第二巻の命題11で定義された外中比から導かれる比率である。その表現は「与えられた線分を二分し、全体と一つの部分に囲まれた矩形を残りの部分の上の正方形に等しくすること」である。
すなわち、図1-2において、「正方形 ABΔΓのAΓの中点Eで、半径EBの円弧からZを求めて、正方形AΘHZと矩形KΔBΘの面積が等しくなるように作図すると、交点ΘはABを外中比に分割する」とされている。 これを数式で検討してみよう。
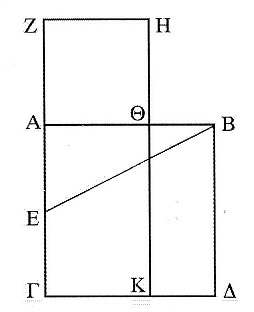
図1-2において、ABを単位長さの1とおいて、AΘ=xとおくと、ΘB=1-x である。
正方形AΘHZと矩形KΔBΘの面積が等しいのであるから、
xx=1-x ……………………(1-1)
すなわち
xx+ x - 1 = 0 ……………………(1-2)
この二次方程式の解は
x = ( √5-1)/ 2 と -( √5+1)/2 である。
前者の解が図1-2の AΘ そのものの長さであって、後者の解の絶対値は外分点のまでの長さ、すなわち、AΘ=1とした場合の ABの長さである。
というのは、φ=( √5-1)/2 ……………………(1-3)
Φ=( √5+1)/2 ……………………(1-4)
とした場合、
Φ=1/φ …………………………(1-5)
だからである。さらにこの φ とΦ の間の関係は、
φ=0.6180339 ……………………(1-6)
であり、
Φ=1. 6180339 ……………………(1-7)
なる、小数点以下が全く等しいという特別な関係にある。すなわち
Φ=φ+1 ……………………(1-8)
である。
読者はこの不思議な数値のことを認識されたい。
さらに図1-2において、AZ=AΘであるから、
ΓA:ΓZ = 1:Φ=1:1. 6180339……
さらに図1-2において、AΓの中点EとBを結ぶと、
EB=√5/2 であり、ΓAを単位長さとすると、
EZ = 1/2 + AZ = 1/2 + AΘ = 1/2 +φ= √5/2 = EB
であるから、点Zは中点EからEBの長さに等しい点として決定できる。
黄金比を作図する方法がここで明らかである。
図1-2上で示すと、単位長さをΓAにとると、正方形ABΔΓを描き、中点Eを中心に長さEBと同じく点Zを決定する。 すると、点Aは長さΓZを黄金分割する。さらに、AZに等しくAΘをとることによって、Θは単位長ABを黄金分割する。
ここで強調するが、この黄金比
1:( √5+1)/2 =1:1.6180339……
または
( √5-1)/ 2:1 = 0.6180339……:1
はここでの骨幹となる事項である。
古来この黄金比は芸術上非常に重要な役を果たしてきている。
パルテノン神殿の破風下の縦横比は黄金比をなす。ミロのヴィーナスの彫像にもその比が見られる (図はGoogleより引用)。

ところで、最も卑近な級数の例は次のようなものである。
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ・・・・・・・・・・・。
つまりある項はその前の二つの項の和で決められる。フィボナッチ数列と呼ばれている。そして、各項がこの極めて単純な法則で決められるこのフィボナッチ数列の、ある続く二つの項の前項を後項で割った値が、不思議なことに、前記の
φ= ( √5-1)/ 2 = 0.6180339……
に収束する、すなわち項が大きくなればなるほど、このφの値に近づくのである。
前述の数学者ルカパチョーリは、ルネッサンス期には黄金分割(黄金比)として知られていた「神聖比例」(divina proportione)すなわち上記 Φ=1. 6180339…… に限りない美学的意味を与えており、その『神聖比例論』に著わしている。
レオナルドは(今で言う)芸術をも学問の一つと考え、さらに「数学的な証明に耐え得ないものは、真の学問は称し得ない」とし、その必要条件として「経験に立脚しなければならない」点と「数量的な証明を伴わなければならない」点をあげている(裾分一弘著『イタリア・ルネサンスの芸術論研究』中央公論美術出版、昭和61年、253ページ)。
レオナルドは人体各部の表現と遠近表現の線遠近法において数学すなわち比例を盛り込むことを強く意識し、その基礎を確固たるものにすることに努めた。その基本は黄金比である。
本サイトではレオナルドが生涯にわたって、この黄金比を追求し、美を求めたことを述べたい。
