第一章 レオナルドの『絵画論』とその比例理論
はじめに
バロックの画家プッサンやカラッチ兄弟、更にはゲーテにまでも影響を及ぼしたレオナルドの絵画論があった。
ヴァチカンの教皇庁立図書館蔵に「ウルヴィーノ稿本」がおさめられており、これは晩年のレオナルドの愛弟子フランチェスコ・メルツィがレオナルドの意図を忠実に再現すべく努めたものとして広く受け入れられており、一般にレオナルドの『絵画論』はこの本の現代語訳を指している。
その一方で、ミラノ在住時代に書かれ、今は失われた「スフォルツァ絵画論」と呼ばれるものがかってあり、その中に「諸芸術比較論」があったと推定されている。ミラノで知己となった数学者ルカ・パチョーリはミラノ公に献呈した「神聖比例論」の献辞で、レオナルドが「絵画と人体の運動に関する書物」を刻苦勉励の末に書き上げたことを伝えている。
またロマッツォなる人物は「諸芸術比較論」でレオナルドは絵画と彫刻のいずれが高級であるかを論じた、と記している。
レオナルドはその「絵画論」の中で「数学的な照明に耐え得ないものは、真の学問と称し得ない」とし、その必須条件で「経験に立脚しなければならない」点と「数量的な証明を伴わなければならない」点を上げている。
しかし、レオナルドの数学的知見は十分には検討されてこなかった。ウィンザー手稿(Windsor 19118v)(図Ⅰ(1) – 5)の「数学者ではない者に、私の原理を読ませてはならない」なる戒めが何を示すのかが課題であった。

図Ⅰ(1) – 5 ウィンザー紙葉19118v 部分拡大図、翻刻
また「ホイヘンス稿本」(ニューヨークのピアモント・モーガン図書館蔵)なる文書が存在し、この中には現存するレオナルドの手稿から、かって転写されたと見られる紙葉が多数あり、多くの研究者によって、レオナルドの手稿との関連、編著者が誰であるか、について研究がなされてきた。
エルヴィン・パノフスキーは1940年に「ホイヘンス稿本」の研究結果を発表した。これはレオナルドの絵画理論を説明した第一の業績とされる。
第一節 レオナルド・ダ・ヴィンチの比例理論
向川博士はレオナルドの絵画理論の研究結果から、人体描写の基本を明らかにした。
その論拠となるのは『ホイヘンス稿本』(Codex Huygens MA1139)である。この稿本の最初の研究は1940年にパノフスキーによって発表されたが、博士はそれをさらに進展させた。
図Ⅰ(1)‐6はホイヘンス稿本第一葉で、参考図Ⅰ(1)‐6はその翻刻である(図番は向川博士の原論文(自費出版)と同様とするので、本サイトでは番号順ではない)。
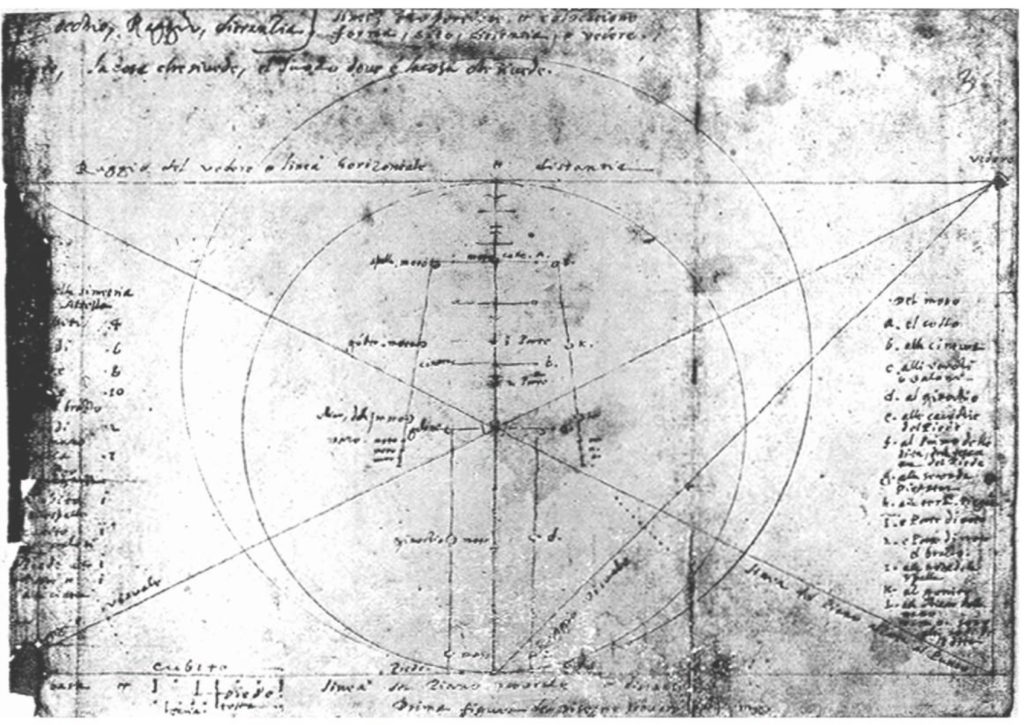
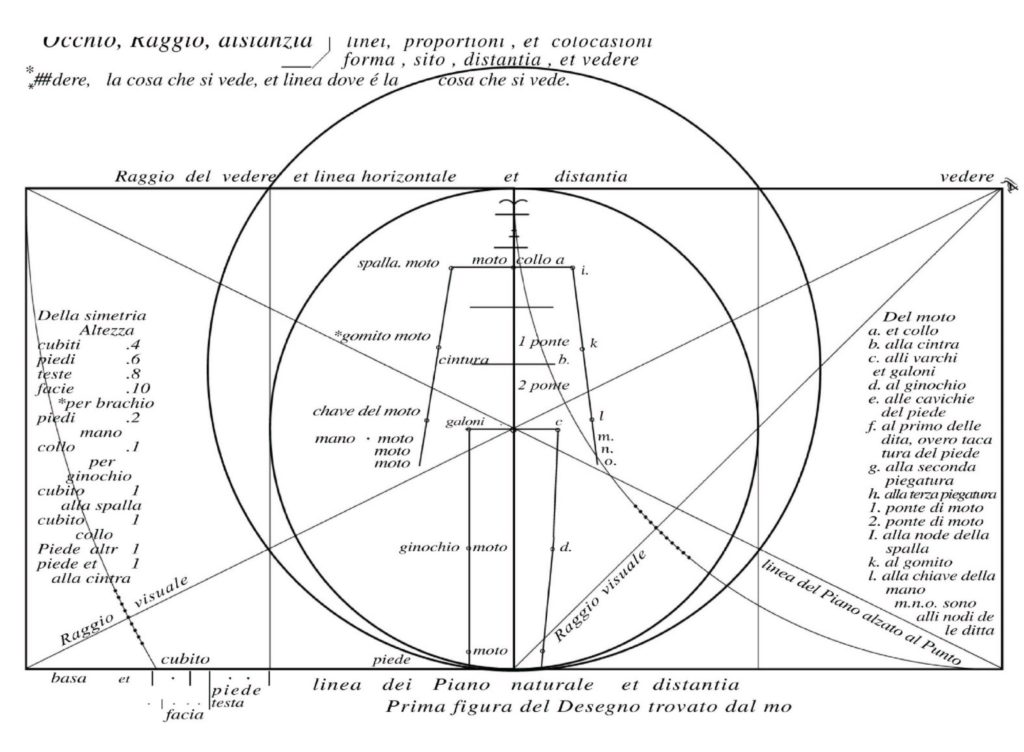
小円の直径は描かれる人体の身長であって、この小円の直径を各々左右の辺とする正方形が描かれ、これらより、1対2の辺の比率の長方形が構成される。大円は正方形の縦の中心線を黄金比で分割する点を中心にして、長方形下辺に接するように描かれる。
ここで強調しなければならないのは、古代ギリシャ彫刻の時代より、人体の表現においてへその位置が身長を黄金分割するという事実である。このことは19世紀半ばにドイツの美学者ツァイジングが述べたことから、一般に広まった。レオナルドの時代には既に知られており、レオナルドもこの例に従ったということである。
長方形右上の眼を象った目印から長方形の短辺(正方形の一辺)と長辺を半径とした二つの円弧が描かれ、正方形の対角線との、および長方形の対角線との交点部が点線で示されている。
「小円」で示された人体は単純な直線で示され、身体各部の比例の基準線が水平線で示されている。
パノフスキーは「大円」をウィトルウィウスの「円」としており、単純な線で表された身体は両足を60度に開いて、腕を伸ばして肩を中心にして水平より30度上に挙げて、翼を拡げた鷲の姿勢を取った場合、この「大円」に接するとしている。
大円の中心はへその位置であり、これは身長を黄金比で分割する点であり、大円の半径は正方形の一辺を単位の“1”とした場合、0.6186……(=φ)である。
更にこの葉には詳細な説明が多々書かれており、紙葉の経年変化と損傷から記文の判読は非常に困難であり、画聖の意図を見抜くのは難かしい。レオナルドの手稿は本来メモの類であり、我々も同様であるが、他人に見せたり、説明のために書き残すものではなく、心憶えである。これをきっかけに考えていたことを思い出す性格のものである。
特に紙葉左側十九行に渡って書かれた人体比例の基準値は、身長に対して各部分の長さが幾つ取れるのかを示した「分数方式」のシンメトリアの尺度で示されている。
第二節 黄金分割とダブル・スクエアのフィオゲネシス
向川博士は、この「ホイヘンス稿本」に、レオナルドが《ウィトルウィウス的人間像》を描くにあたって黄金比を適用したことの幾何学的手法を見出し、ダブル・スクエアのフィオゲネシスと名付けた。その数学的説明は、この節の最後に示すが、要点を表すと下記のようになる。
辺の比が1:2の長方形の対角線上に黄金比 φ(=0.6186……)の比率の線分が形成される。
すなわち挿図4(原論文ではp14)において、GC:FG:EF:AE = 1: φ:φφ:φφφ である。対角線上に順に黄金比の等比級数が構成されているということである。
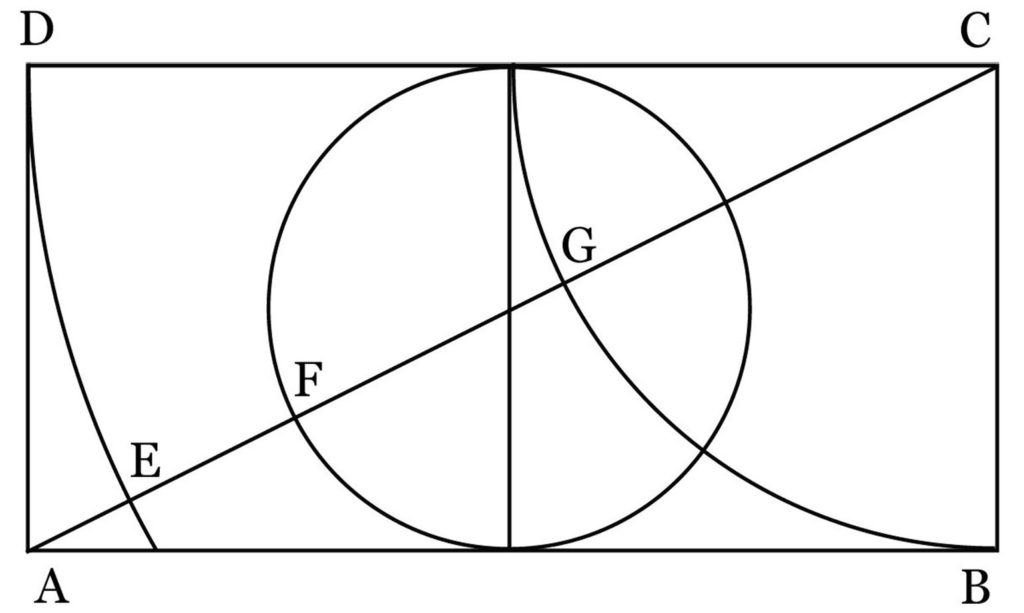
絵画画面において、上記の長方形と黄金比の等比級数を成す線分を用意しておくと、容易にこの比率の線分を描くことが出来る。
レオナルドはこの幾何的真理を発見し、絵画構成に厳密な黄金比の尺度を導入したのである。
画家は画面を構成する際、特定の線分の黄金比の割合での拡大・縮小をこのダブルスクエアのフィオゲネシスを用いて行うことができる。レオナルドはこの原理を用いて人体各部の長さ、目・鼻・口等の位置を決定した。
モナ・リザの顔がレオナルドの顔と、それらの目、鼻、口の位置が全く同一であり、絵画の像は自分の顔を写した如くに言われるのは、それらの位置がこのような法則で決定されることにより、当然の帰結なのである。
話を「大円」に戻そう。パノフスキーはこれをウィトルウィウスの円と呼び、腕を上げた人体像を囲むものとした。ウィトルウィウスの人体図の代表とも言われる「レオナルドの人体権衡図」(本サイト最初の論文の概要の最初の図を参照)にも、これに相当する円が描かれている。しかしこのレオナルドの場合の円は、ホイヘンス稿本の大円とは異なっている。
この差異のことは後に説明するが、「レオナルドの人体権衡図」の円は人体を描いた後にそれを囲むが如くに描かれたように見えるが、それは事実ではない。画聖レオナルドは絵画を厳密に数学的な帰結として描いたのである。
下記ダブル・スクエアのフィオゲネシスの項では、現在の我々の数学の表示で示したのではあるが、レオナルドは、その原理を発見したのである。
レオナルドの「絵画論」は机上の空論ではなく、経験に裏打ちされた実用性と数学的証明性を兼ね備えたものであって、それらがミラノ期以降の絵画作品に実現されていくのである。
当時は φ や π (パイ) などの記号をつかってはいないから、無理数の扱いが現在のようにはいかない。ミラノの宮廷で無理数の計算を学んだ数学者ルカ・パチョーリとの邂逅は比例理論の進化のための大きな転換点になったことが分かっている。
ダブル・スクエアのフィオゲネシス
挿図4において、円の中心(長方形の中心)にOと記号を付け、長方形ABCD中に対角線AC上に単位長1の半径の円との交点G、直径1の円との交点F、半径2の円との交点をEと取る。
φ=(√5- 1)/2 は XX + X – 1 = 0 の解であるから、φφ=1-φ
GC=1 FG=FO+(OC-GC)=1/2+(√5/2-1)= (√5- 1)/2=φ
AE =√5-2
EF=AO-AE-FO = √5/2-(√5-2)-1/2= (3-√5)/2=1-(√5- 1)/2=1-φ=φφ
AE =√5-2 = 2× ((√5- 1)/2) – 1 = 2φ- 1 = φ- φφ = φ(1-φ)= φ×φφ= φφφ
よって GC:FG:EF:AE = 1: φ:φφ:φφφ
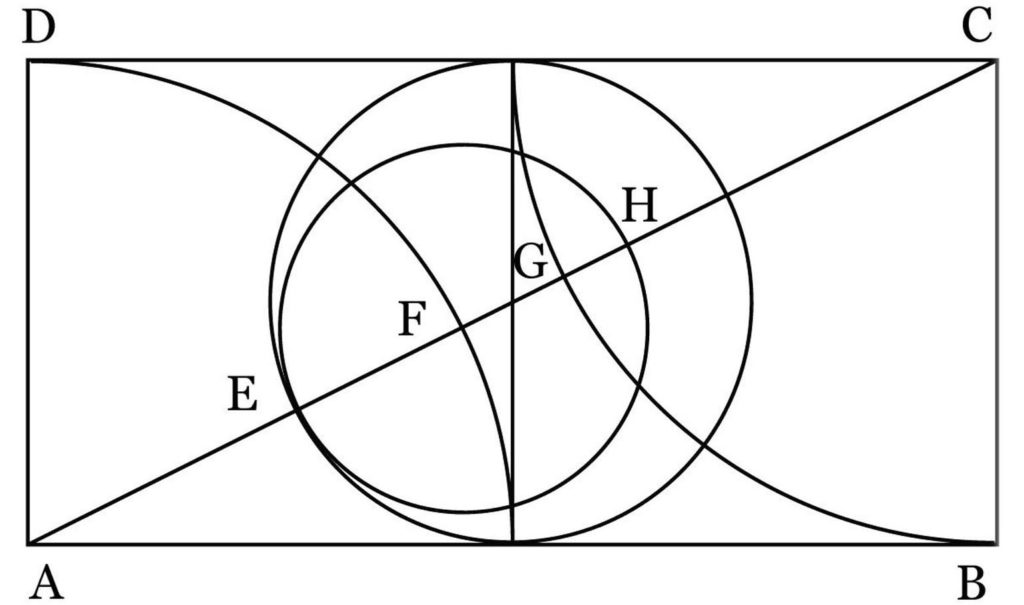
同様な論理によって、挿図5の系において、AE:EF:FG:GH=1: φ:φφ:φφφ が導き出される(詳細は原論文p15に記載されている)。