第三章 レオナルドのリテラルな記述と問題点
第一節 パラゴーネにおける「神聖比例」の解釈について
パラゴーネにおける「神聖比例」
今日レオナルドの『絵画論』(Trattato della pittura) として知られている書物の原本となった「ウルビーノ稿本」(Codex Urbinas Latinus 1270) 、グリエルモ・マンツィによってローマ法皇庁立図書館で発見、の第一章はパラゴーネ (paragone) と呼ばれている。
パラゴーネはレオナルドの芸術観を示したものとして知られており、他の芸術と比較したとき、どれほど絵画が学問としての基礎を持っているのかを示している。ここでは、パラゴーネに書かれている「神聖比例」が黄金分割を意味することを明らかにする。
レオナルドの『絵画論』も他と同様実技書であるが、現存する『絵画論』はレオナルドの死後、愛弟子のメルツィ(1493-1570) が編纂したものである。そこに述べられている線遠近法等の基礎となる幾何学は、三次元空間を二次元の画面に投影する画家にとって、重要なものである。
向川博士のレオナルドの《人体権衡図》の研究以前の定説は、レオナルドの比例理論を音楽的な調和比例に基く分数システムを考えるものであった。
パラゴーネには美しい顔のプロポーションについて記されていて、 ‘divina proportione’ なる言葉があるが、このプロポーションに係わった形容詞 ‘divina’ がレオナルドの人体比例との関連で検討されてこなかった。
パラゴーネでは、「神聖比例」が美しい容貌にあり、かつその容貌は「調和のとれたプロポーション」を持っているとしている。レオナルドは楽器リラの名手であって、音楽の基礎となる調和比例が人体比例理論の基礎であることを知っており、美しい容貌の「調和のとれたプロポーション」を顔面部の「調和比例」と読み換えることが可能で、パラゴーネの記述は純然たる数学的な意味を持ってくる。
レオナルドの人体比例研究
ウィンザー王立図書館収蔵の「解剖手稿」のウィンザー紙葉12601( 図Ⅲ(1)-1)とヴェネツィア・アカデミア美術館収蔵の紙葉236 番( 図Ⅲ(1)-3,4) を取り上げ、レオナルドの記述した「調和比例」と「神聖比例」を検討する。これらの図の記文には、頭部・顔面各部の寸法が詳細に記述されている。ウィンザー紙葉12601( 図Ⅲ(1)-1)は、ペドレッティなどのレオナルド研究家によると、ほぼ1488年から90年にかけた時期に描かれたと推定されている。ヴェネチア・アカデミア美術館収蔵の紙葉236番( 図Ⅲ(1) -3、4)については、紙葉236表の下部のスケッチは、ジョヴァンナ・ネピ・シレーが後日1503年頃《アンギアーリの戦い》のアイデアを描き加えたものとの新説を発表した。
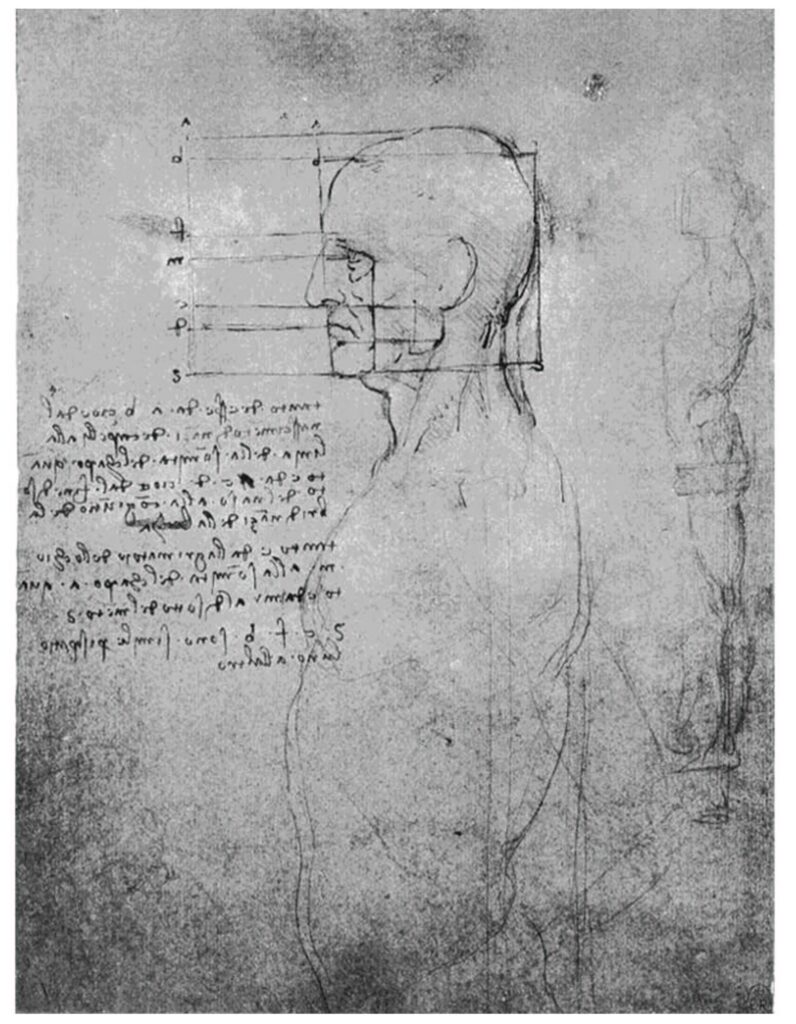
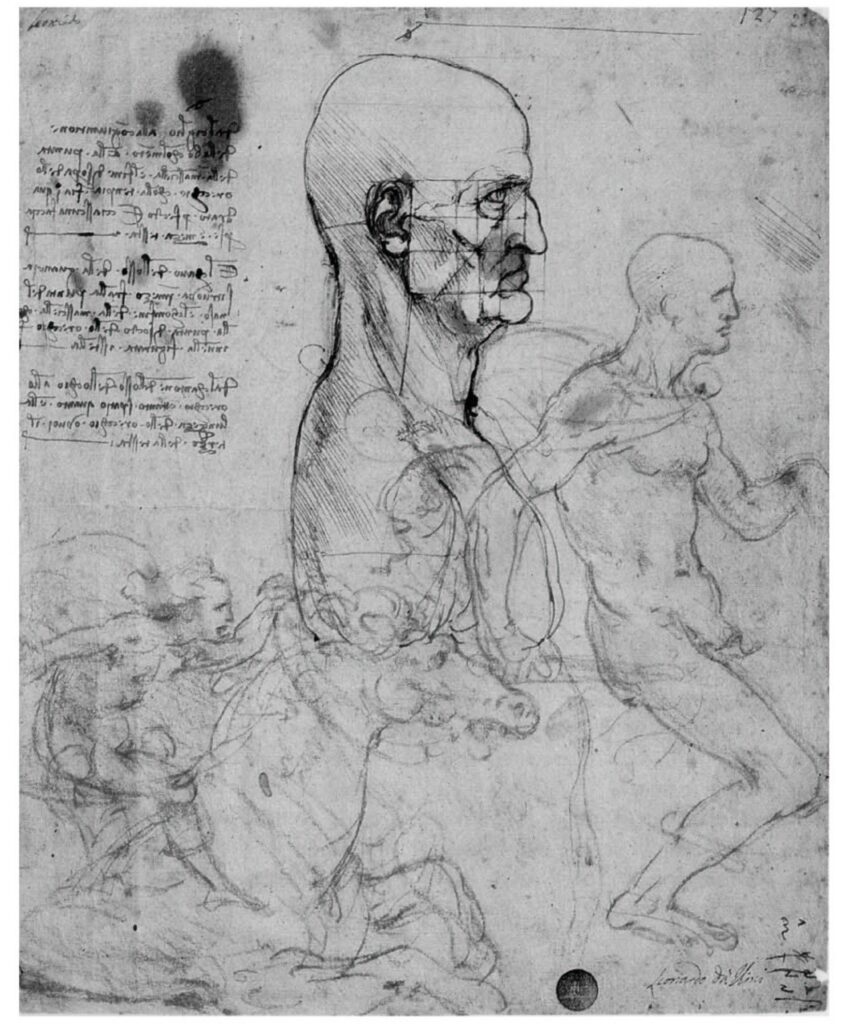
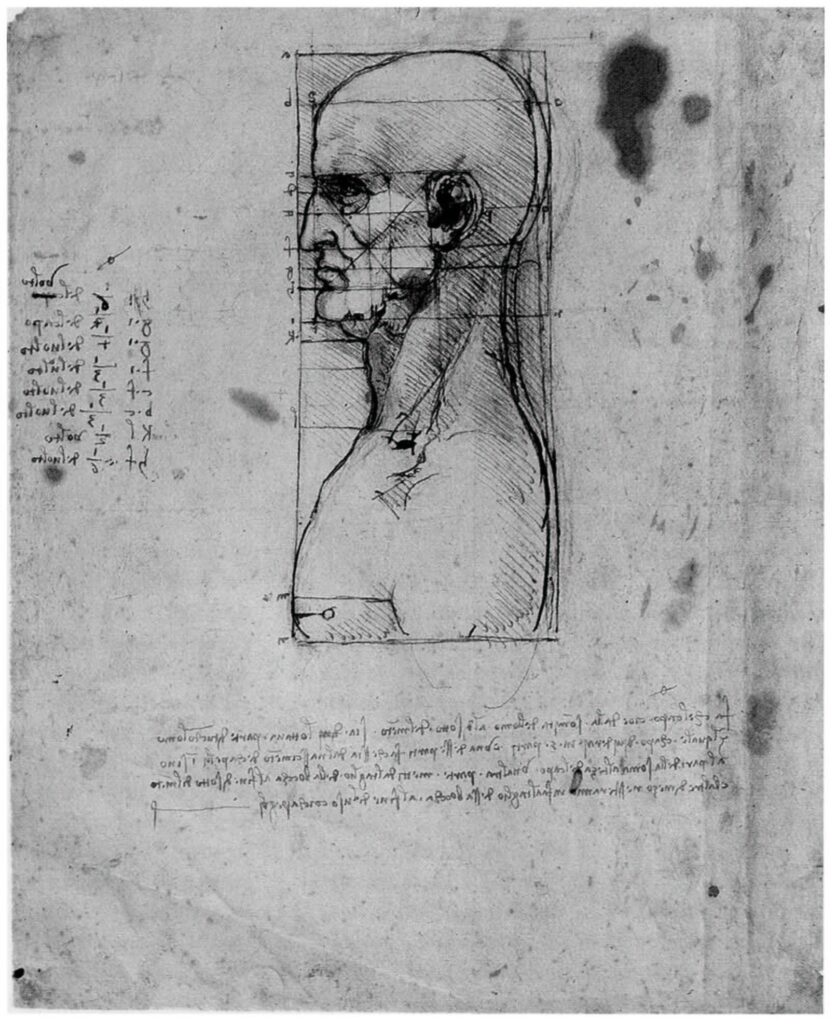
レオナルドの人体比例理論はミラノ時代の「スフォルツァ絵画論」にまとめられたと推定されているが、現在は失われた。ウィンザー紙葉12601(図Ⅲ(1)‐1)およびヴェネチアのアカデミア美術館の紙葉236番 (図Ⅲ(1)‐3、4) とウィトルウィス的人間を描いた紙葉228番の《人体権衡図》(図Ⅱ(1)-1)は貴重な原資料である。
ジュゼッペ・ファヴァロは頭部について詳細な検討を行った。表2は黄金分割の関係を示したもので、レオナルドが描いた頭部の比率は表のイタリック体の数値のように明らかにフィボナッチ数列{1,2,3,5,8,13,・・・・}が使われていることが判る。
フィボナッチ数列は黄金比に収束するから、レオナルドは顔面構成を黄金比に沿って行ったと言うことができる。
表2)ファヴァロに見られるフィボナッチ数列(斜体)の位置
――――――――――――――――――――――――― ―――
口の上 1 :鼻中隔下部から唇の会交部
頤 2 :口の下の窩から頤下部
頭皮 2 (3) :頭頂から髪の生え際
口の下と頤 3 :唇の会交部から頤( 下部)
額 4 :髪の生え際から眉毛の間
鼻 4 :眉間から鼻中隔( 下部)
鼻と口の上 5 :眉間から唇の会交部
頚部 6 :頤下部から頚窩
額と鼻 8 :鼻中隔下部から髪の生え際
鼻と口と顎 8 :眉間から頤
頤と頚部 8 :頤下部から頚窩
眼から頚部 13 :内眼角から頚窩
頭高 15 (16 )* :頭頂から頤下部―――――――――――――――――――――――――――
(* 印はアカデミア紙葉236番の頭高の数値を示す)
図Ⅲ(1)-6に示したように、α・β・γ・δは黄金比の等比数列を作っている。

パラゴーネには、「調和比例を成すもの」が「同時に全体が結合して神聖比例を成しており」(15r)、更に各部を纏めた「神聖比例を成すものにのみ美が存在し」(18r) 、「神聖比例を構成して調和比例を成すもの」(11v-12r) に、美しい容貌の比率がはっきり存在することをレオナルドが謳っており、「神聖比例」を黄金分割として使っているのである。
第二章第一節で見たように、向川博士の研究によれば、《人体権衡図》( 図Ⅱ(1)-7) で2と5を初項とする線形回帰数列 {2, 5, 7, 12, 19…} がフィボナッチ数列の代わりに使われていたが、これがファヴァロの研究にフィボナッチ数列以外の比率が含まれる理由で、《人体権衡図》を作図する際、レオナルドがウィトルウィウスの基準に従い身体各部の規準線に黄金比の等比数列を使った理由である( 図Ⅲ(1)-8)。従って、ファヴァロの研究とレオナルドが《ウィトルウィウス的人間像》で黄金比の等比数列を使ったことは良く符合するのである。
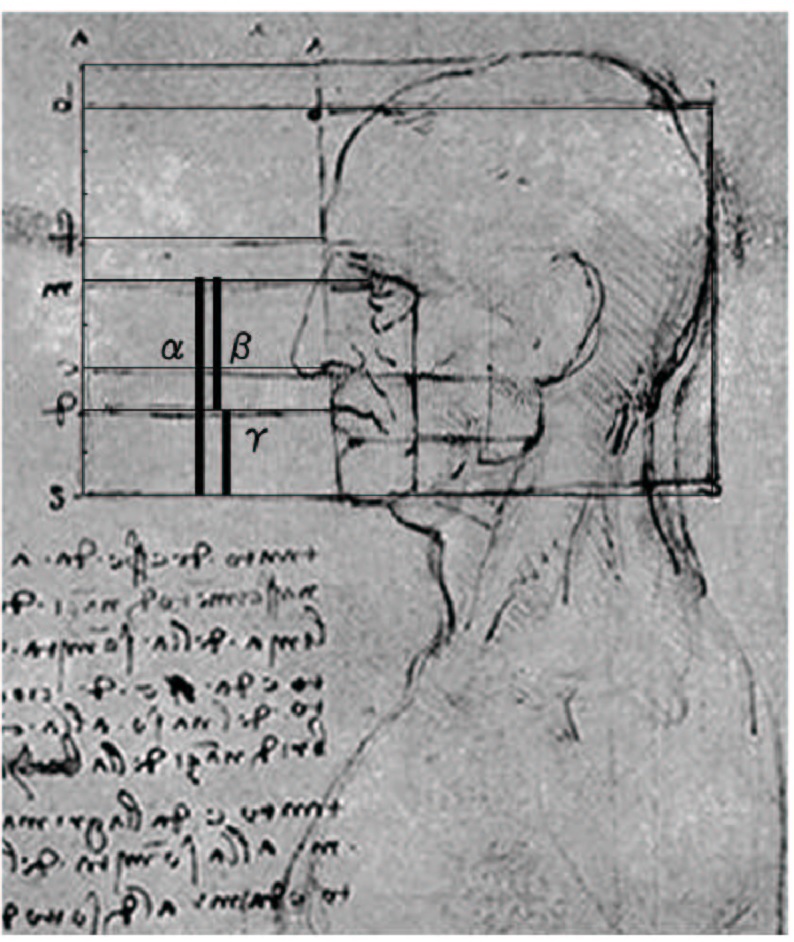
図Ⅲ(1)-7 で、α・β・γ の比率は多少誤差があっても黄金比の等比数列になる。それ故このウィンザー紙葉12601においても「神聖比例」すなわち黄金比で描かれていると言える。表3でレオナルドは頭部の各部の比率を実際は無理数ながら、概数で示したと言える。
表3) ウィンザー紙葉12601 (頭高の1/10 を単位とする比率) ――――――――――――――――――――――――――――――
頭皮 1
額 3
鼻;眉間から鼻の底面まで ( 眉間から内眼角は1 単位) 3
口の上 1
口から頤の下 2
――――――――――――――――――――――――――――――
計 10
レオナルドの《人体権衡図》の身体各部に見られる黄金比の等比数列が、ウィンザー紙葉12601およびヴェネチアのアカデミア美術館の紙葉236番の頭部の比率を示した規準線にも存在する。
ケンプ博士は 《人体権衡図》にコンパスの痕を指摘しているが、これらコンパスの痕は黄金比の等比数列をこの図の中に作図してゆくために必要だったのである。
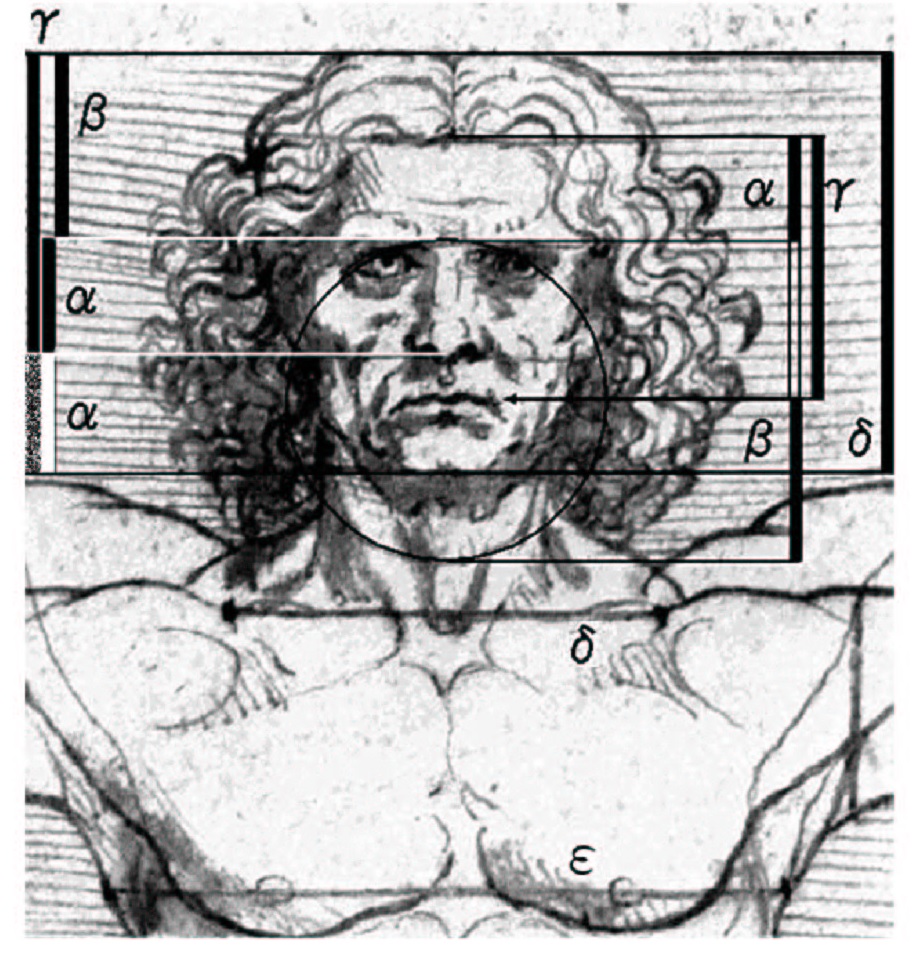
《人体権衡図》には、ウィンザー紙葉12601 やアカデミア紙葉236番と同様、唇の先端にはコンパスの痕があり、頭部の各比率を決める規準点だったことが判る 。このことは、唇の先端を中心にして眉間までの長さを半径とする円を描いたとき、頚部に残された円弧がこの円に一致することから確かめられる。この半径の長さをβ とすると、α・β・γ・δ・ε は黄金比の等比数列の各項を形作り、δ の長さが頭高と一致している( 図Ⅲ(1)-8)。
表4)《人体権衡図》の線形回帰数列(斜体)の位置 ――――――――――――――――――――――――――――――
額、鼻、上口部から頤 α: ( 顔の1/3) 4
上唇先端から眉の位置 β: ( 顔の1/2) 5
上唇中央から髪の生え際; 頭頂から鼻の底面 γ: ( ——- ) 9, 10, 11*
頤から頭頂まで; 胸の上端の規準線の長さ δ: ( 頭 高 ) 14, 15*
乳頭の高さの規準線の長さ ε: δ×1.618… ——- ――――――――――――――――――――――――――――――――
( ) 内は記文の数値、* 印はアカデミア美術館紙葉236 番の頭皮の数値によるもの
既述ケンプ博士は指摘していないが、上記の二つの紙葉での唇の先端の他にも、《人体権衡図》には δ とε とで示したコンパスの痕が黄金比の比率となる二つの線があった。レオナルドは、この二つの線分について《人体権衡図》の記文では何も記載していない。しかし、これは身体各部の比例の基準として、胸の上端の規準線が頭部の長さδ に等しくまた乳頭の高さの規準線ε が体幹の幅を示すことから、体系的に扱っていたと判断される。
従って、ここでもケンプ博士の指摘するコンパスの痕は、他の素描と対照するために付けたものではなく、《人体権衡図》の比例体系に準拠してレオナルドが意識的に使用したものと考えるべきだろう。《人体権衡図》の頭部と胸部に見られる各部の大きさはファヴァロの数値に対照した場合、上掲の表4のようになるから、斜体で示した頭部の各部の比率 { 4, 5, 9, 14…} もまた、フィボナッチ数列と同様、黄金比の極限値になる初項{ 4, 5 }による線形回帰数列になっている。
制作時期の問題点
制作年代については、定説では、ヴェネチア・アカデミア美術館の所蔵する《人体権衡図》が1490年から92年前後であり、アカデミア美術館紙葉236番が一般的な定説では1490年頃とされており、またウィンザー紙葉12601が1488年から90年にかけた素描と推定されている。
パラゴーネに書かれた美しい容貌に存在する「調和比例」と「神聖比例」とによって、頭部の比例関係に黄金分割が考えられていたことが判る。 レオナルドは、マクマホン版パラゴーネ第28節「画家と論争した詩人へのマティアス王の答え」で、「調和比例」と「神聖比例」が美しい容貌に結びつくと論じている。
そしてマティアス王が存命の時期(1490年4月死去)とウィンザー紙葉12601を含む初期の人体比例研究の時期が重なっているから、この一節が1480年代末の「学問の決闘」 (duello) を反映するのであれば、1496年にミラノに来たルカ・パチョーリと出会う以前からレオナルドが「神聖比例」という言葉を黄金分割として使っていたことを示すはずである。
レオナルドのパラゴーネは絵画を学問として扱い、「絵画学」(scienza della pittura) の基礎を自由学芸 (Liberal Arts) の中の幾何学に代表される数学的な四科 (Quadrivium、算術、幾何、天文学、音楽のこと) に置いている。イルマ・リヒター女史が指摘したように、これはレオナルドが中世以来の自由学芸の伝統と如何に対峙していたのかを示している。レオナルドは1480年代のミラノの宮廷で盛んに行われた芸術の比較論争において、視覚的芸術と絵画が本質的に備えた特質(virto)を第二の「自然」と考え、学問的な根拠を視覚的に自然を再現する数学的比例関係に求めていたことがパラゴーネの記述から判る。レオナルドは当時の先端技術、遠近法とウィトルウィウスの人体比例理論に基づく学問として「絵画学」を確立すべく戦っていたことを示している。
向川博士の検討によれば、これら①アカデミア紙葉236番表、②ウィンザー紙葉12601、③アカデミア紙葉236 番裏、④《人体権衡図》の描かれた時代的順序は、この番号順であって、《人体権衡図》の頚部に残された円弧(図Ⅲ(1)-8)もレオナルドの検討の痕と推定される。
向川博士は以下のように推定している。アカデミア紙葉236表は最も早い時点の作品で、従来通り1485年から89年頃の初期の解剖学研究に属する素描だろうが、裏面とは制作時期が異なるものと考えられる。第二番目のウィンザー紙葉12601は紙葉12637と直接対照されることから定説通りになり、1489年の解剖学的研究のウィンザー紙葉19059と同じ時期になる。前章のように《人体権衡図》が1500年代のアンギアーリ期以降になるので、アカデミア紙葉236裏面は《人体権衡図》よりも前になることは確かで、アンギアーリ期に属するものと見ることができるであろう。
ウィンザー城に残された「解剖手稿」に、レオナルドは「数学者でない者に、私の原理を読ませてはならない」(Windsor 19118v)( 図I(1)-5) と書いている。ハイデンライヒはこれを解剖学関係の手稿について述べたものと考えているが 、レオナルドの人体比例理論を再検討する上でこの記述は非常に大きな意味を持っている。何故なら、今日でも解剖学の中で数学と直接関係を持つのは人体比例論しかなく、チェンニーニ以来、ルネサンス期には多くの「芸術論」が書かれたが、それらは自然を模倣し再現することを目指して、実際に幾何学を運用するための技法書的性格が強かった。
ハイデンライヒの示した上掲のレオナルドのウィンザー紙葉の記述は、人体比例論を含んだ解剖学関係および「絵画学」に関連した記述として見ることができる。本稿で取り上げたように「ウルビーノ稿本」のパラゴーネには、数学的には未検討のまま残されていた「神聖比例」の問題があった。ウィトルウィウスに基づく《人体権衡図》の規準線が黄金比の等比数列と一致することと併せて、パラゴーネの「神聖比例」は黄金分割を表すことが明らかになったであろう。パラゴーネの記述の中で、「調和比例を成すもの」(l’armonia proportionalità) が結合すると、「神聖比例」(divina proportione) が生じるとされており、ここで取り上げた三つの素描はそれぞれ調和比例と黄金分割を満たすことから、数学的な意味でも充分合理的な記述とすることができる。
パラゴーネに書かれた美しい容貌の各部には、ピタゴラスの言う「調和比例」と「神聖比例」が共通に存在し、レオナルドが著作を読ませる対象を明確に数学者に限定していることから、「私の原理」と呼ぶものには何ら定説が無い以上、ハイデンライヒ説と併せて「調和比例」と「神聖比例」の問題を捉え直す必要があった。本稿で取り上げたパラゴーネの記述は、レオナルドの「絵画学」の数学的モチーフとして黄金分割の概念が1480年代末から存在していたことを示している。
第二節 レオナルドの黄金分割と《superbipartienti》
問題としての比例理論
遠近法研究として、日本においては、辻 茂教授と篠塚二三男教授の新たな研究が上げられる。中世ヨーロッパの絵画はキリスト教の教義の絵解きとして存在し、線遠近法や人体比例論を必要としなかったが、ルネサンスの芸術家は数学的基盤の上に古代ギリシャ・ローマの芸術作品に匹敵する作品を作り出している。
人間の手で創られた第二の自然である絵画が、対象の三次元的数量関係を二次元の絵画面に写すために必要としたものが、これらの比例理論であった。
レオナルドの線遠近法については種々の解釈があり、《最後の晩餐》の室内についても多くの解釈が提示されていて、その差異は画聖がルネッサンス時の「正統作図法」(construzione legittema) に寄っていたものと考えられる。
芸術作品に内在する比例関係を規定する命題で、黄金分割の問題を取り上げたのは、ルカ・パチョーリの『神聖比例論』が最初とされてきた 。しかし、前節で見たように、レオナルドの人体比例理論にはこの比率の等比数列が見られた。加えて、レオナルドの『絵画論』の序文に相当するパラゴーネの中の「神聖比例」という言葉は、黄金分割を示すことが確かめられる 。
ここでは比例理論のクロノロジカルな検討をする上で、発展段階の指標となるアルベルティが「誤った遠近法」と記述するものを取り上げ 、《最後の晩餐》に使われたレオナルドの線遠近法の作図システムの成立時期とその発展の順序を検討する準備としたい。
黄金分割と外分割
黄金分割は、19 世紀半ばにドイツの美学者ツァイジングが古代ギリシャ彫刻の身体各部の比率を示すために用いたことから一般に広まった言葉で、19 世紀前半からドイツで数学用語として使われている(図Ⅲ(2)-3)。この言葉は「オームの法則」で有名な物理学者ゲオルグ・オームの弟マルチン・オームの数学の教科書に使われたのが初出で、比較的新しい数学用語である。
ダン・ブラウンの『ダ・ヴィンチ・コード』が2003 年に出版されて、その作品に記された秘密に脚光が当てられている。 日本でもレオナルドの作品や素描と手稿の内容に改めて関心が集まっている。
ここでレオナルドの暗号とされたものは、古代ローマの建築家ウィトルウィウスの記述に基づいた音楽的調和比例の身体区分を指している。ダン・ブラウンの小説の解説本等に見られる人体比例の説明は、レオナルドが黄金分割をどのように扱ったのかほとんど説明しておらず、また誤った部分も含まれている。
向川博士の分析図に見られるように黄金分割の作図が、《最後の晩餐》の画面でこの使徒の配置決定に用いられている。画幅を8等分した正方形のモジュールで 3対5 に分割する位置にマクダラのマリアとされる人物が位置しているだけでなく、 キリストの傍ですぐ右側の天を指差すトマソの指の先端が、キリストの右のこめかみの消失点を通る水平線と黄金分割の作図のための弧線の交点に位置していることが判る( 図Ⅲ(2)-4) 。

《最後の晩餐》の構図に見られる黄金比は、1971 年のトーマス・ブラチャートの論文が初出だが、その指摘は音楽的調和比例について触れた部分で単に言及しているに過ぎず、問題そのものは認識されていなかった( 図Ⅲ(2) – 5) 。しかし、ブラチャートの指摘した音楽的調和比例は正当なもので、レオナルドの《最後の晩餐》の室内空間の構成を検討する基礎となっている。

そこでレオナルドの人体比例理論と《最後の晩餐》の線遠近法に跨がった黄金比とその等比数列の問題を取り上げたい。この問題は美術史における重要な概念だが、従来、正確な解釈の無かったブルネレスキの活躍した時代の線遠近法を反映する数学概念 《superbipartienti》、 即ちアルベルティの記述する「誤った作図法」を示す用語が黄金比を意味することを説明する。
ルネッサンスにおける黄金分割
既に述べたように、1490年代初めに書かれたレオナルドの『絵画論』の序文に相当するパラゴーネで、これまでは明確に定義できなかった「神聖比例」という言葉は、黄金比を示すことが明らかとなった。この記述はレオナルドがパチョーリと邂逅する以前に書かれたと推定されているので、パチョーリの『神聖比例論』以前からフィレンツェの芸術家の間で黄金比が知られていたことを示唆している。
さらに、ルカ・パチョーリの著作『神聖比例論』のプラトンの正多面体は、レオナルドが描いた図を使用しているので、 これはレオナルドが黄金比を知っていたことの証左でもある。
黄金比はユークリッドの『原論』に述べられている。 しかしこの書は当時のイタリアの芸術家やその徒弟たちに読まれたとは考えられ難い。 さらに、ルネッサンス期では無理数の表現がまだ無く、 たとい黄金比がユークリッドの『原論』に述べられていたとしても、それを数学的に表す適切な方法が無かった。
ではどのように表現されていたのであろうか。
芸術家やその関係の職人達に知られたであろう、レオン・バッティスタ・アルベルティの著書『絵画について』に語義の不明瞭な《superbipartienti》なる言葉があり、これが黄金比を示す言葉であれば、レオナルド以前から黄金比が知られていたとすることの文字による証拠となる。
向川博士は 《 superbipartienti》に含まれる単語要素分析から、「外分割」を意味するとしている。
この単語は1491-2年出版のボエティウスの『著作集』の中の『音楽論』にある。
ボエティウスの『音楽論』は、中世からルネサンスにかけて直接伝えられていなかったピタゴラスの音楽理論を伝える原典の役割を当時担っていたもので、アルベルティや次章の《最後の晩餐》で扱うレオナルドの 《superbipartienti》 の学問的源泉と考えられるものである。
ピタゴラス音階の音程と調和比例との関係から、単弦琴の弦を区切る長さの問題が数と数量関係で論じられている。この外分割の図解(図Ⅲ(2)-10) は、ピタゴラスの音階理論から解説したもので、音階が弦長を簡単な整数比で分割することで得られることを示している。
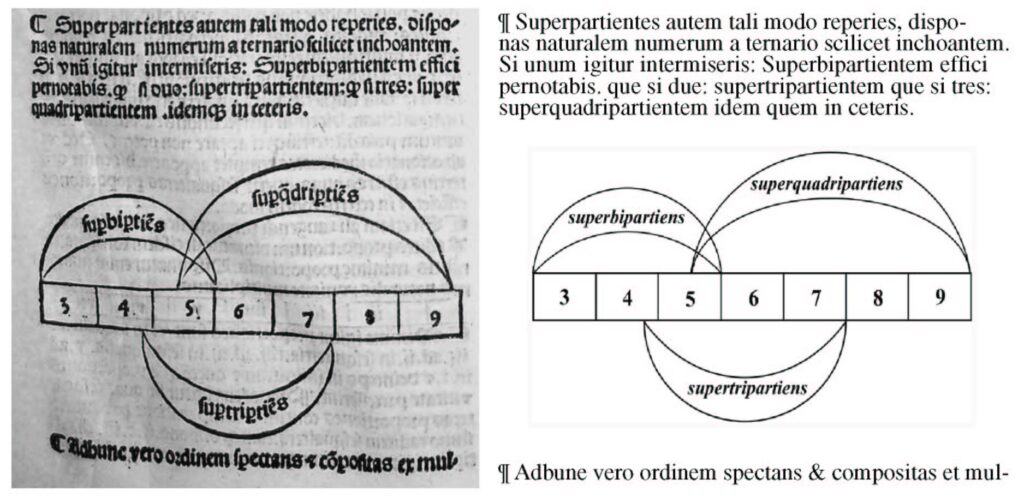
実際この数学概念は、レオナルドにとっても難しいものだったと見え、マドリッド手稿II の第四十八葉裏から第五十葉表にかけて、アルベルティの「誤った作図法」の記述の中にあった 《superbipartienti》がある。そして、1504 年頃の記述とされるアトランティコ紙葉331r に「根の乗法について、ルカ師に尋ねること」と書いているように、《最後の晩餐》を描いていた頃に、レオナルドが未だ無理数を代数的に扱うことができなかったことにも呼応している。
《superbipartienti》は裾分教授が指摘するように 当時のフィレンツェの画家達の間で1ヶ3分の2として知られていたと見ることができるだろう。
