Mathematics in the Leonardo Era and Golden Ratio
What was the situation like in mathematics in the time of Leonard’s living Renaissance? Today, the state of the art in mathematics has reached a level that most ordinary people cannot understand, but it can be said that mathematics of that era is understandable to the general public of present days.
For more details on the history of mathematics, leave it to another book (Boyer “History of Mathematics 3”). Let’s take a look at it.
Mathematics originated in Mesopotamia and Egypt and was accepted by the Hellenistic civilization and made great strides during the Greek era. After that, there was no great progress until the time when Leonardo lived in the late Middle Ages, and further academic progress must wait for Galileo and Newton to appear. It can be said that humankind has since made explosive progress in this field. At present, the state of the art in mathematics is far beyond what the general public can understand.
The year after Leonardo’s birth 1453 Constantinople fell due to the Islamic army attack. It is said that the Western European world came into contact with ancient heritage because ancient Greek books were transmitted to Italy by exiles. It also means that they have lost their reliable source of supply (Boyer “History of Mathematics 3” p1). Prior to that, books were first printed in Western Europe in 1447. However, few were mathematically proficient enough to publish Greek geometric classics.
Irrational numbers were already known in the 400 years BC, but it can be said that they had little need in general life. The symbolic system has not yet been adopted as simple as it is now. In other words, these expressions have been developed in algebra and the symbolic system after Leonardo’s era, from the 16th century onwards. It is after Descartes (1596-1650) that the expression “√” was used as it is today.
The economic situation at that time was in the era of the Mediterranean trade, and efficient numerical expressions for stockpiling, trading, and clearing of trade goods were required. It is an era when the widely used decimal and scale techniques have begun to spread.
After Fibonacci, a 13th-century mathematician Leonardo da Pisano, introduced Arabic mathematics to Italy, Philippine Brunelleschi, Leon Batista Alberti and Piero dera Francesca and others acquired the viewpoint of reproducing a three-dimensional space on a picture screen using geometry against the background of the most advanced mathematics in Europe.
The geometry studied by these intellectuals and artists was always closely related to two issues. One was their problem of “reconstruction of classical antiquity”, the problem of human proportion based on Vitruvian Man, and the other was “linear perspective” to transform three-dimensional real world to two-dimensional plane like a mirror, which would open the era of modern science.
It can be said that these problems were concrete geometric problems of how to determine the proportional relationship together, as typified by Leonardo’s “Vitruvian Man”.
Leonardo had a strong desire to explore nature and was excellent at observing. It extends to the mathematics field, and Leonardo became acquainted with Luca Patchouli, a talented mathematician at the time at the court of Ludovico Il Moro, Duke of Milan.
Luca Patchouli (1445-1517) was a monk of Saint Francesco, who made a name for himself in the works “Summa de Arithmetica,Gemetria,Proportioni et Proportio-nalita” and “De Divina Proportione”, which summarized mathematics during this period. Especially in the latter, one of the purposes was to complete the mathematical foundation of art. Piero della Francesca (1412-1492), better known today as a painter, made outstanding achievements in mathematics during this period. Patchouli included the work of Piero della Francesca in his book “Summa de Arithmetica,Gemetria,Proportioni et Proportio-nalita”.
Leonardo gained his knowledge of cutting-edge mathematics at the time from Patchouli. On the contrary, he worked as an illustrator in Patchouli’s book “De Divina Proportione” and drew many pictures of various kinds of polyhedrons. Through such companionship, Leonardo explored ways to take advantage of mathematics to personalize his knowledge of mathematics and enhance its beauty in painting. However, Leonardo may not be said to have made outstanding achievements in the field of mathematics (Boyer “History of Mathematics 3”). But in 1998, Irle and Schröer revealed in a paper that Leonard calculated π with an accuracy of 1/10000.
Golden Ratio
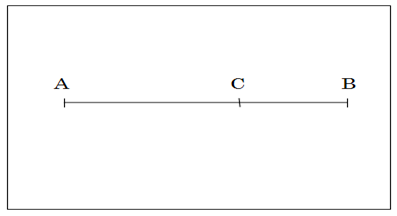
In Fig. 1-1, dividing the line segment AB at the point C such that AB:AC = AC:CB is called “golden division”, and the ratio 1:(1+√5)/2 is “golden ratio” Also, dividing by this ratio is called the golden division.
The expression of this number is of course modern, and this “golden ratio” itself has been defined since the Greek era. That is, it is the ratio derived from the outside-center ratio defined in Proposition 11 of the second volume of Euclid’s “Elements”. The expression is “to divide a given line into two parts, and to make the rectangle surrounded by the whole and one part equal to the square above the rest”.
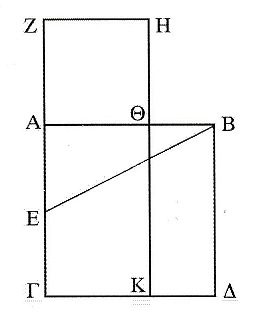
In other words, in Fig. 1-2, “At the midpoint E of A Γ of square AB ∆ Γ, find Z from the arc of radius EB and draw so that the area of square A Θ HZ and rectangle K ∆B Θ are equal, and intersection Θ divides AB by outside-center ratio.”
Let’s consider this with a mathematical formula.
In Fig. 1-2, if AB is assumed to be unit length 1 and AΘ=x, then ΘB=1−x. Since the area of the square AΘHZ and the area of the rectangle KΔBΘ are equal,
X2=1-X (1-1)
That is
X2 + X-1 = 0 (1-2)
The solution of this quadratic equation is
X = (√5−1)/2 and −(√5+1)/2
The former solution is the length of AΘ itself in Fig. 1-2, and the absolute value of the latter solution is the length up to the externally dividing point, that is, the length of AB when AΘ=1. It is because if
φ=( √5-1)/2 (1-3)
Φ=( √5+1)/2 (1-4)
Then
Φ=1/φ (1-5)
Furthermore, the relation between φ and Φ are
φ=0.6180339…… (1-6)
Φ=1.6180339…… (1-7)
There is a special relationship that the numbers after the decimal point are exactly the same, i.e.
Φ=φ+1 (1-8)
The reader should be aware of this mysterious figure.
Further, in Fig. 1-2, AZ=AΘ, so
ΓA:ΓZ=1:Φ=1:1.6180339…… (1-9)
Further, in Fig. 1-2, when connecting the midpoints E of AΓ and B,
EB=√5/2, and letting ΓA be the unit length, then
EZ=1/2+AZ=1/2+AΘ=1/ 2 + φ = √5/2 = EB,
point Z can be determined as a point where EZ equals to EB.
The method of plotting the golden ratio is clear here.
As shown in Fig. 1-2, when the unit length is ΓA, a square ABΔΓ is drawn, and the point Z is determined around the midpoint E as the length EB. Then, point A divides the length ΓZ by golden ratio. Furthermore, by taking AΘ equal to AZ, Θ divides the unit length AB by golden ratio.
It is emphasized here that this golden ratio
1 : (√5+1)/2 =1 : 1. 6180339………… (1-10)
or
(√5-1)/2 : 1 = 0.6180339…… : 1 …… (1-11)
is the key issue.
Since ancient times, this golden ratio has played a very important role in art. The aspect ratio of the Parthenon temple under the gable is the golden ratio. The same ratio can be seen in the statue of Venus de Milo.

By the way, an example of the most familiar series is as follows.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34……
That is, a certain term is determined by the sum of the two terms before it. It is called the Fibonacci sequence. Then, the value obtained by dividing the previous term of the following two terms by the latter term of this Fibonacci sequence in which each term is determined by this extremely simple law is, strangely, φ = (√ 5-1)/ 2 = 0.6180339……, that is, the larger the term, the closer to this value of φ.
The above-mentioned mathematician Luca Pacholi gave the divina proportione, which was known as the golden ratio during the Renaissance, i.e. Φ=1.6180339… , in his book “De Divina Proportione”.
Leonardo considered that art (so called now) was one of the academic disciplines, and further stated that “what cannot withstand a mathematical proof cannot be true academic”, and the necessary condition were “it should be based on experience” and “it should be accompanied with proof”.
Leonardo was strongly aware of the inclusion of mathematics, or proportionality, in the perspective of the representation of parts of the human body and the perspective, and sought to solidify the foundation. The basis was the golden ratio.
In this site, the author would like to state that Leonardo pursued this golden ratio and sought beauty throughout his life.
