第二章 レオナルドの人体比例理論と問題の発見
第一節 レオナルドの《人体権衡図》その「円」と「正方形」について
ウィトルウィウスはローマの建築家で1世紀の人である。
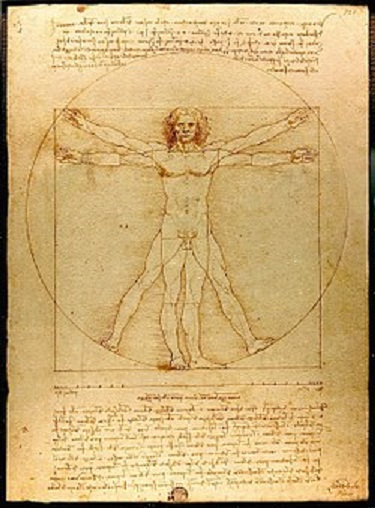
ルネサンス期において、ウィトルウィウスの『建築十書』は古典古代ギリシャ・ローマの建築理論を伝える唯一の技法書として建築家のみならず、他の諸分野の芸術家からも広く関心を寄せられた。ルネサンスの芸術家は、ここに書かれていた神殿建築の比例についての記述を古典古代の人体比例論としてとらえて、多くの《ウィトルウィウス的人間像》と呼ばれる作品を残している。いずれもこの建築書の第三書第一章の記載に基づいて描かれたものであり、ヴェネチアのアカデミア美術館が所蔵するレオナルドの《人体権衡図》(図Ⅱ(1)-1)は、その中で最も良く知られたものということができるであろう。
20世紀になると欧州各地に保存されていた手稿が順次出版されてゆくにつれて、「近代的な科学者」としてのレオナルド像が形作られていったと言えるが、この動きに従って、レオナルドの人体比例論も数量的な分析の対象とされるに至っている。それらの数量的な比例理論に関する研究には、ジュゼッペ・ファヴァロやルドルフ・ウィットコーワのものが上げられる。これらの研究が身体各部の比例関係や、そこに現れる「調和比例」の問題を取り扱っているのに対して、レオナルドの人体比例研究を包括的に示した業績は、エルヴィン・パノフスキーの『ホイヘンス稿本とレオナルド・ダ・ヴィンチの絵画理論』をもって嚆矢とされるであろう。
ルネサンスの芸術家たちはウィトルウィウスの記述の中に古代ギリシャの美の規範があると考え、その記述と整合性を持った人体像を作ることを目指した。具体的には「円」と「正方形」が与えられて、《ウィトルウィウス的人間像》を描きだすということである。
ここでは、レオナルドの素描に描かれた規準線と、向川博士がホイヘンス稿本第一葉中に発見した幾何学に基づく事実とから、人体権衡図の「円」と「正方形」を決定する方法を述べる。
森田慶一博士の訳によるとウィトルウィウスの記述とは、下記のようなものである。
『 神殿の構成はシンメトリアから定まる。この理法を建築家 は十分注意深く身に付けなければならぬ。これはギリシャ語でアナロジアといわれる比例から得られる。比例とはあらゆる建物において肢体および全体が一定部分の度に従うことで、これからシンメトリアの理法が生まれる。実に、シンメトリアまたは比例を除外しては、すなわち容姿の立派な人間に似るように各肢体が正確に割りつけられているのでなければ、いかなる神殿も構成の手段をもちえない。
実に、自然は人間の体を次のように構成した。—頭部顔面は顎から額の上毛髪の生え際まで10分の1、同じく掌も手首から中指の先端まで同量。頭は顎からいちばん上の頂まで8分の1、首の付け根を含む胸のいちばん上から頭髪の生え際まで6分の1、<胸の中央から>いちばん上の頭頂まで4分の1.顔そのものの高さの3分の1が顎の下から鼻孔の下までとなり、鼻も鼻孔の下から両眉の中央の限界線まで同量。この限界線から頭髪の生え際まで、額も同じく3分の1。足は、実に、背丈の6分の1、腕は4分の1、胸も同じく4分1。その他の肢体もまた自分の計測比をもち、昔の有名な画家や彫刻家たちはそれを用いて大きな限りない称賛を博したのである。
これと同様に、神殿の肢体は個々の部分を総計した全体の大きさに最も工合よく計測的に照応しなければならぬ。人体の中心は自然に臍である。なぜなら、もし人が手と足を広げて仰向けにねかされ、コンパスの先端がその臍に置かれるならば、円周線を描くことによって両方の手と足の指がその線に接するから。さらに、人体の円の図形がつくられるのと同様に、四角い図形もそれに見いだされるであろう。即ち、もし足の底から頭の頂まで計り、その計測が広げた両手に移されたならば、定規を当てて正方形になっている平面と同様に、同じ幅と高さがそこに見いだされるであろう。(以下略) 』
古代の復興を目指したルネサンスの芸術家にとってウィトルウィウスの記述は、理論上の典拠として意義を持った。プロポーションの問題は多くの場合建築のおける比例理論や遠近法と密接な関連を持っている。このことは彼らにとって中世以来の学問の伝統の中で、数学的科目である四科と伍して芸術が自由学芸に比肩し得るものであった。ウィトルウィウスから伝えられた古代ギリシャの身体美を再現する調和比例の理論はその規範であった。
リオネロ・ヴェントーリは次のように述べている。
『 ルネサンスのイタリアの芸術家たちが欧州に君臨するのは、彼らが比例と遠近法の効果を算出するすべを知っていたためである。そのうえ彼らは、ギリシャやローマの古代人が、その著述のみならずとくにその造形作品に発揮した自然についての知識を利用する。これらの遺物は、イタリアにおいて他の欧州のどの地域よりもすぐれた質のものが数多く存在し、また発掘されていたのである。 』
一方で元のウィトルウィウスの記述は判り難いもので、他のルネサンスの芸術家のそれと同様に、その「円」と「正方形」の説明の合理性に議論があり、極端にはそれらは伝説にすぎないとの論もでた。その背景にはオイラーやカントールなどの数学者が試みた研究でも合理的な説明が付けられていないこともあった。
レオナルドの《人体権衡図》は身体の各部比例関係が最もウィトルウィウスの基準値に近いものとされる。
レオナルドの《人体権衡図》
レオナルド・ダ・ヴィンチの《人体権衡図》とは、図Ⅱ(1)-1の広く知られ、かつレオナルドの代名詞とも言ってよい図のことである。
レオナルドが描いた人類の至宝とも言うべきこの図面はヴェネツィアのアカデミア美術館の所蔵されており、我々に均衡のとれた人体の調和の美を感じさせる。
アラーノ女史によると、図は金属筆、栗色のインク、および水彩が使用されており、向川博士の私見によると、人体の頭部、手、腋の下、足許などの水彩とされる部分はインクを筆で彩ったものであろう、人体像にはウィトルウィウスの基準に合せて、人間の体勢を区分する線がインクで引かれている、と。
人体像の下に、円と正方形と同じ栗色のインクで基本尺度を記した直線が引かれている。この図像の上下に参考資料に示す記文が記されている。
《人体権衡図》は内容や図と記文の形式から見ると、レオナルドが人体の素描を中心にして、紙面全体として一つのシェーマ(形式・体系・枠組み)を形作るように考えていたことを示している。
記文の翻刻には代表的なものに二つがあるが、文法上の解釈に若干問題があるようである。図には身体各部の比例関係、レオナルド自身の「円」と「正方形」の作図方法が示されている。作図方法が示された下に、身体各部の比例関係を示した人体が「円」と「正方形」に内接するように描かれている。下に書かれた記文は、ウィトルウィウスの記述をそのまま書き写したものではなく、レオナルドの解釈に基づく身体各部の比例関係を示したものであり、《人体権衡図》に描かれた身体各部の比例関係を説明するものとなっている。レオナルドの《人体権衡図》の構成上の形式はユークリッド幾何学の命題・特述・作図・証明という証明形式に模式化できる。
《人体権衡図》記文
命題 建築家ウィトルウィウスはその建築論の中で人間の寸法は自然によって次のように配分されていると述べている。すなわち、指四本は掌一つになり、掌四つは足一つになる。掌六つはクビト(*)一つになり、クビト四つの身長になる。またクビト四つは一歩になり、掌二十四は身長になる。そしてかれの建築にはこれらの寸法が用いられる。(*中指の先端から肘まで)
特徴 もしも高さが身長の14分の1減少するように両脚を開き。また両腕を広げて頭頂の水平線に中指が接するまでに挙げれば、広げた四肢の各先端の中心が臍に当たり、両脚の間にできる隙間が正三角形になることを知らねばならない。
《ウィトルウィウス的人間像》の作図と基本尺度
作図 ―――――――――――――――――――――――――――――――――
|指|掌| 人が両腕を広げた長さは身長と同じである |指|掌|
証明 髪際から顎の先端までは身長の10分の1である。顎の先端から頭頂までは身長の8分の1である。胸の上端から頭頂までは身長の6分の1になる。胸の上端から髪際までは全身長の7分の1になる。乳首から頭頂までは身長の4分の1になる。肩の最大幅は身長の4分の1に当たる。肘から手の先端までは身長の4分の1になる。肘から肩の端までは身長の8分の1になる。手全体は身長の10分の1になる。性器の位置は身長の半分に当たる。足は身長の7分の1になる。足許から膝下までは身長の4分の1になる。膝下から性器までは身長の4分の1となる。顎から鼻までの部分と、髪際から眉までの部分は、それぞれ耳の長さに等しく、また顔の3分の1である。
レオナルド・ダ・ヴィンチの《人体権衡図》について、図の上に記述されたウィトルウィウスの規準によると、足の大きさは身長の6分の1になることが導き出される。
レオナルドの図には、身長各部の比例を示す線が書き込まれていた。しかし、記述中にウィトルウィウスの基準には書かれていない身長の7分の1という数値があった。しかもその値は、レオナルド自身のウィトルウィウス解釈を示したと考えられる下の記文に限られている。
つまり、レオナルドの記述はウィトルウィウスの規準と異なっているということなのである。
これらの記述の中で「胸の上端から髪際まで」という部分に引かれた規準線に注目すると、臍の位置は左足の親指との間で「黄金比」の近似値となることが計測により明らかになる。さらに、詳細に計測すると、「黄金比」はこの他にも《人体権衡図》に書き込まれた規準線上に確認できる。以下の一覧表で示したものは「黄金比」の近似値になる規準線の位置である。《ウィトルウィウス的人間像》の図の「円」の中心となる臍を起点として見た場合、これらの規準線の位置は人体に外接する「円」と臍との間で、黄金比(1.6180……)を公比とする等比数列になっていることが判る。この等比数列と筆者の推定の基礎となった実測値を次の一覧表で示す。
l1 (臍~乳頭間) 25.5 mm = k ≒ 7
l2 (臍~胸の上端) 40.5 mm = k×Φ ≒ 12
l3 (臍~髪の生え際) 66.5 mm = k×Φ×Φ ≒ 19
l4 (円の半径) 109.5 mm = k×Φ×Φ×Φ ≒ 31
∴ l1 : l2 :l3 :l4 = 1 :Φ:Φ×Φ:Φ×Φ×Φ
≒ 7 : 12 : 19 : 31
黄金比をギリシャ文字 Φ で表し、臍と乳頭の間を単位長 k とする。
この表から明らかなように《人体権衡図》の比例の規準線は、その一部が Φ の等比数列と重なっている。そしてその数列は線形回帰数列(先に述べたフィボナッチ数列はその一つ)、すなわち隣り合った二つの数の和が次の数になっていて、この隣り合った二項の比の極限値は黄金比に収束する。
これまで、このウィトルウィウスの規準とレオナルドの記述の差は、ウィトルウィウスが伝えた足の比率が大き過ぎるので「身長の6分の1」から「身長の7分の1」に変えたと今日まで考えられてきた。しかし、レオナルドが足の長さの基準を単に自然に即して決めたのではなく線形回帰数列の要素を使ったと考えた場合、「身長の7分の1」という記述はこの数列{ 2, 5, 7, 12, 19, 31,…… }の要素となるため、臍を起点とする黄金比の等比数列と密接な相関関係が出現する(図Ⅱ(1)-7)。従って、《人体権衡図》を実測した値と、レオナルド自身が与えている下の記文の身体各部の比例の基準値から、図に引かれた比例の規準線の位置は「黄金比」を利用して決められたものと考えられる。
このようにレオナルドは数学的な基準をもって絵を構成したと言えるのである。

次に《人体権衡図》の円と正方形について述べよう。 ホイヘンス稿本の研究の嚆矢とされる論文を発表したパノフスキーによると、この図の「大円」は、ウィトルウィウスの記載した「円」とされており、その論拠にレオナルドの方法が引用されている。即ち「両足を60度のなす角で広げ、外側に拡げた腕を30度上に挙げて、翼を広げた鷲の姿をしたとき、大円は臍を中心として手足の指の先端に接するように描かれる」という記述は、レオナルドが書いた《人体権衡図》の記文を説明するものに他ならない。しかしながらこの「円」が如何なる幾何学的メソッドで決定されているのか、パノフスキーの解説では何も説明されてはいない。
ホイヘンス稿本の第一葉(図Ⅰ(1)‐6)に描かれた幾何的な要素を見直すとき、そこにはパノフスキーが説明していない幾何学的な意味を持った点線が描かれていたが、先に述べたように、第一章の挿図4はこの点線が如何なる意味を持つかを説明した図である。既に述べたように、長方形の対角線上の長さのCG、GF、FE、EAは黄金比の等比数列を為しているのである。そして、この第一葉の大円は挿図4のAG(2φ)を直径とする円なのである。それ故この円の中心は中心線(単位長さ1)を黄金分割することになる。
読者にはこの円は中央の正方形の上端の二点を通り下辺に接する円と解する向きがあるかも知れない。が、そうではないのである。この円の上辺の切片を計算する(付録参照)と、約 0.9550 と計算され、殆ど 1 である。数学的に厳密な検証ができない場合には真実は見えない。レオナルドの言葉「数学者でない者に、私の原理を読ませてはならない」(Windsor 19118r (ウィンザー紙葉 19118r ))の意味内容を読み取る必要がある。レオナルドは黄金分割を用いていることを、あからさまには述べていないのである。
しかし、レオナルドの《人体権衡図》の手を伸ばした人体を囲む円は実はこのウィトルウィウスの円ともまた異なるのである。
ではレオナルドはどのようにして、この円を定めたのであろうか。
図Ⅱ(1)-10は、マドリッド手稿第八十一葉面で、レオナルドが《人体権衡図》の「円」の直径を求めた図である。参考図Ⅱ(1)-10で説明すると、二種類の扇形の内、大きい方は人体を囲む「正方形」の外接円の一部であり、正方形の底辺から扇形の頂点までの高さがレオナルドのウィトリウィウスの円の直径となる。


従って《人体権衡図》の「円」と「正方形」は次のように記述できる。
「正方形」に外接する円と内接する円を描いたとき、この双方に接して、かつ
「正方形」の底辺に接する円がレオナルドの《人体権衡図》の「円」である。
正方形を古代ギリシャの四大として捉えるならば、レオナルドのウィトルウィウスの「円」は「マクロコスモスの大宇宙とミクロコスモスの人体を繋ぐ円環」と評することができる。
[ 付録 切片の長さ ]
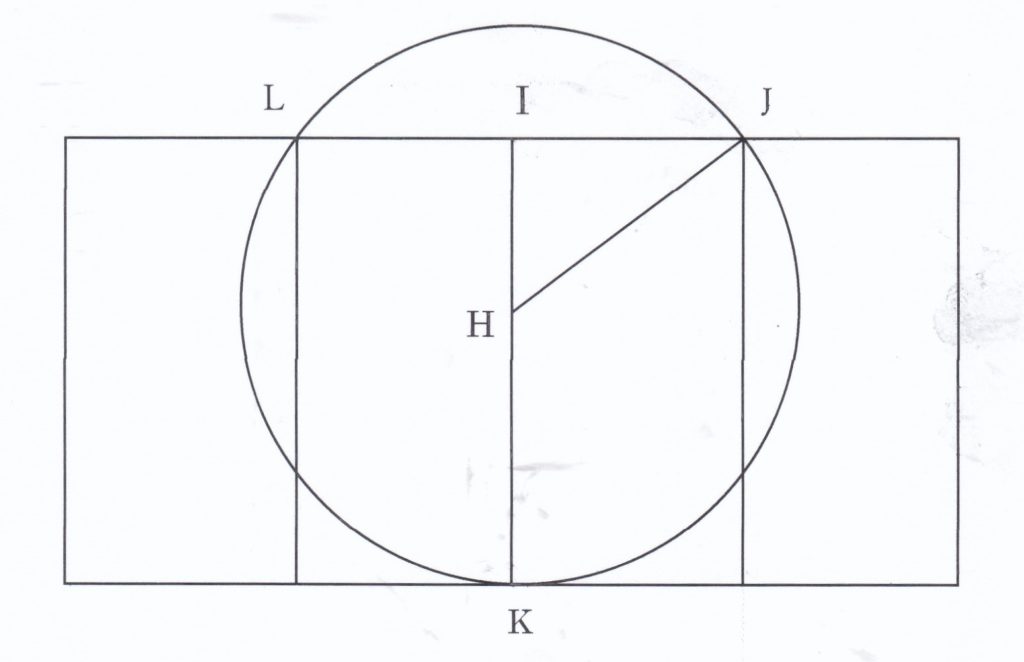
付図において正方形の一辺K Iを単位長さとすると、H(へその位置)はK Iを黄金比に分割するから、HK=0.61803……、HKを半径とする円(ウィトルウィウスの円)の上辺との交点をJ、Lとすると、
(HJ)2=(HI)2 + (IJ)2
HI = 0.38196……を代入すると、 IJ = 0.4775……と算出される。
すなわち、LJ = 0.9550……となる。
これに対し、レオナルドの《人体権衡図》においては、同様な正方形の上辺での人体を囲む円の切片は 0.9102……と算出される。
第二節 レオナルドのウィトルウィウス的人間像の変遷
ドイツの美術史家クラウス・イーレと画家クラウス・シュレーアはレオナルドがその《人体権衡図》を元に極めて正確な円周率を求めていたことを1998年に明らかにした。
このことはレオナルドの《人体権衡図》の円には単に人体を囲むだけの円ではなく、厳密な数学的意図があることを示唆した。
レオナルドは古代から問題となっている等面積の円と正方形を求めることに腐心し、かつそれを《ウィトルウィウス的人間像》の「円」を描くことに関連づけた。
アルキメデスは円に内接する正多角形と外接するそれとの関係から、
223/71 < π < 22/7 (即ち、3.140840……< π < 3.142858……)
と求めている。この方法はギリシャ時代以来二千年の永きにわたり踏襲された。
レオナルドは「私は寸分違わず円を正方形にする」とウィンザー紙葉12280rに記述している。
画聖が熱心に幾何学の問題に取り組んでいたことを示すエピソードがある。マントヴァ公妃イザベッラ・デステの代理人、カルメリ会修道院長、フラ・ピエトロ・ダ・ノヴェッラーラが1501年のレオナルドの消息を伝えるところによれば、レオナルドはこの幾何学に熱中し、絵筆をほとんど手にしなかったということである(アトランティコ手稿167r‐b)。
また、マドリッド手稿Ⅱ-112表に「聖アンドレの夜(1504年11月30日)、灯火も、夜も、また書いてきた紙も尽きるころ、ついに円の求積法を発見した。時間の最後に、結論を得た」とも記している。
しかし、大数学者ガウスも取り組んだ「円の正方化」は直接コンパスと定規で導く方法は無く、1882年にリンデマンが π が超越数であることを証明すると、ユークリッド幾何学の範囲で等面積の円と正方形を決定することは近似値以外には不可能なことが明らかとなった。レオナルドの記述はやはり近似値の範囲内でのことであった。
イーレとシュレーアの研究では、《人体権衡図》の「円」の直径は 2φ (1.2361……) としたのであるが、向川博士は第二章第一節で述べたように、その直径は、(√2+1)/2 即ち1.2071……であるとした。
博士は《人体権衡図》の身体各部の比例の規準線上に黄金比の等比数列を認めたが、この等比数列とウィトルウィウスの記述する音楽的調和比例の基準が同時に成立するためには、レオナルドが与えた「円」の直径 (√2+1)/2 の値が必要になってくる。
アトランティコ手稿 167r‐b 等手稿中の多数の幾何学的作図はこの円を決定するための試行錯誤と考えられる。
ホイヘンス稿本第七葉
レオナルドが考察したと考えられる人体構図の変遷中にホイヘンス稿本第七葉がある。
これはレオナルドが数学的に厳密に人体を描こうとした証左の一例である。描く過程は該7葉において、手足を拡げた人間像を区画する正方形―→それを45度回転(同時に六角形の頂点a が定まる)―→正方形の下辺の2個の点d が定まる―→これらの点d を通る六角形の頂点である下点aが定まる―→六角形の最上点と最下点が定まり、六角形の外円(大円)が確定する。
-766x1024.jpg)
大円の下点を通り正方形の上辺に接する小円が確定し、人体の身長が定まる。左右に頭の高さに上げられた腕は指先が正方形と大円が交差するあたりに位置するように描かれる。この大円の直径は正方形の辺を1 として、1.1849…… と計算される。
レオナルドはアトランティコ紙葉120r‐dに「根の乗法について、ルカ師に尋ねること」と記しているように、これらの幾何形態から身体各部の比率を求めるためには、無理数 √2 や √3 の計算が必要であり、レオナルドの考察はそこまで進んでいたことが明かされている。
表1 は各部の比率をまとめたものである。

第七葉は人体を描いてそれに正方形や円を当て嵌めたものではなく、幾何学的に割り出された比率と位置関係を基に人体を描いたものであった。
このホイヘンス稿本第七葉では、各種の正多角形が表されており、人体の各部の位置がその関連で描かれている。足の位置の高さについても《人体権衡図》とは異なっており、レオナルドの思考が時代々々で変わっていることが理解される。
ルネサンス期の《ウィトルウィウス的人間像》について多くの研究者がその年代を探求しているが、向川博士はこの稿本第七葉の複数の正多角形は、パリ手稿Bの第十二葉裏から第十四表の円に内接する正多角形(図Ⅱ(2)-11から14)やウィンザー紙葉12542r‐v(図Ⅱ(2)‐15)に結びつくから、レオナルドの原図が1490年から92年頃に描かれたものと推定している。

オックスフォード紙葉
ホイヘンス稿本第七葉の作図過程を考える上で参考になるのが、オックスフォードのクライスト・チャーチ図書館蔵の素描である。これらはホイヘンス稿本との強い関連が指摘されている。

レオナルドの《人体権衡図》の「円」とこれらの図のそれらの違いがレオナルドの思考の変遷を示している、と考えられる。オックスフォード紙葉がホイヘンス手稿第七葉と《人体権衡図》を結びつける「ミッシング・リンク」の役割を果たしているとの見解がある。
像の左肩から右上に伸びる直線で示された左腕が正方形の右上隅まで達しており、手の先端は、頭頂よりも高い位置となり、ホイヘンス稿本第七葉やヴェネチアの《人体権衡図》の位置よりも高く描かれている。
左腕と、ホイヘンス稿本第七葉のそれと同じように拡げた両脚は直線で描かれる。拡げた右足の直線はへその位置を通って肩峰まで延ばされている。
図中には左下の腕の図に示されている腕の長さを基準とする尺度cubitoや、手掌の尺度のFacio等の長さを使って、身体の両側に目盛りが記されている。
パノフスキーやイルマ・リヒターがウィトルウィウスの円と称している、これら図の大円について、向川博士は身長を単位長とすると、ホイヘンス稿本第七葉の大円の直径は、1.1849……で、オックスフォード紙葉では 1.236……(=2φ) と指摘している。これらには極めて大きな数学的パラダイムの違いが存在する。言い換えると、レオナルドはこれら時期の異なった絵図において、ウィトルウィウスの円の大きさについて、明確に異なる数値を考えていたということである。
逆に、向川博士が、ホイヘンス稿本第七葉とオックスフォード紙葉の「大円」を同じ大きさに調整して描いた図Ⅱ(3)-1を見ると、正方形が同じ位置に同じ大きさで描かれることが分かる。更にこの図から、オクスフォード紙葉では、人体のへそから上を縮めて描き、八頭身の人体比例に合わせたとも考えられる。

更に、オックスフォード紙葉では、へその位置が身長に対し黄金比の点となっており、ホイヘンス稿本第一葉と同じに描かれている。すなわち、へそを中心とする大円の半径は身長を単位として √5-1 (=2φ)である。
我々は、これらの紙葉を比較することにより、ウィトルウィウス的人体図描写について、レオナルドの考え方の変遷を窺うことができる。
上記の三つの紙葉は ①近似値で扱った時期、②黄金分割の時期、③黄金比の等比数列の時期の三期にそれぞれが対応するはずである。
ホイヘンス稿本第七葉は、各種の正多角形を描き、それらに規定される人体像をウィトルウィウスの述べた描写法、すなわち《人体権衡図》記文の(証明)に述べられた寸法で描く。従って人体像の各部は近似値で扱われる。
オックスフォード紙葉では、へその位置が身長に対し黄金比の点にある。
さらに進んで、レオナルドの《人体権衡図》では、身体各部は音楽的調和比例で規定され、先の図Ⅱ(1)-7に示すように、へそと身体各部の三本の規準線間と円の半径について、四つの黄金比の等比数列の各項が見出される。
レオナルドは第二章第一節のレオナルドの作図法と「円」と「正方形」で述べたように「円」を決定した後、ホイヘンス稿本第一葉のダブルスクエアのフィオゲネシスの法則に則り、四つの黄金比の等比級数を成すように、円の半径を元として、へそと身体各部の三本の規準線の位置を定め、それに基づいて人体像を描いた、と結論づけられる。 レオナルドの《人体権衡図》では前二者(ホイヘンス稿本第七葉とオックスフォード紙葉)よりも数学的に重要な意味を含ませ、精緻な方法で描画が行われている。
第三節 レオナルドとチェザリアーノ版ウィトルウィウス人間像
オックスフォード紙葉の人体図は、ホイヘンス稿本第七葉と、両者の「大円」「正方形」を同じものとし、へその位置が身長を黄金比に分割するように人体を描き直したものであった。
パウロ・セガツォーネが描いたチェザリアーノ版の「円に従う人間」(図 Ⅱ2 -4)と「正方形に従う人間」( 図 Ⅱ2 -5)の絵がある。1490年代には、レオナルド自身人体像をこのように独立したそれぞれ別の素描として表現したと推定される。チェザリアーノ版の「円に従う人間」は描写力が拙い(レオナルドではない人物が意図を理解せず写して描いたと推定される)せいか、レオナルドとの結びつきは注意が払われていなかった。
これらの絵はレオナルドの人体図が最終的な絵図、フィレンツェのアカデミア美術館に所蔵される《人体権衡図》に至るレオナルドの思考の過程を示していると考えられる。
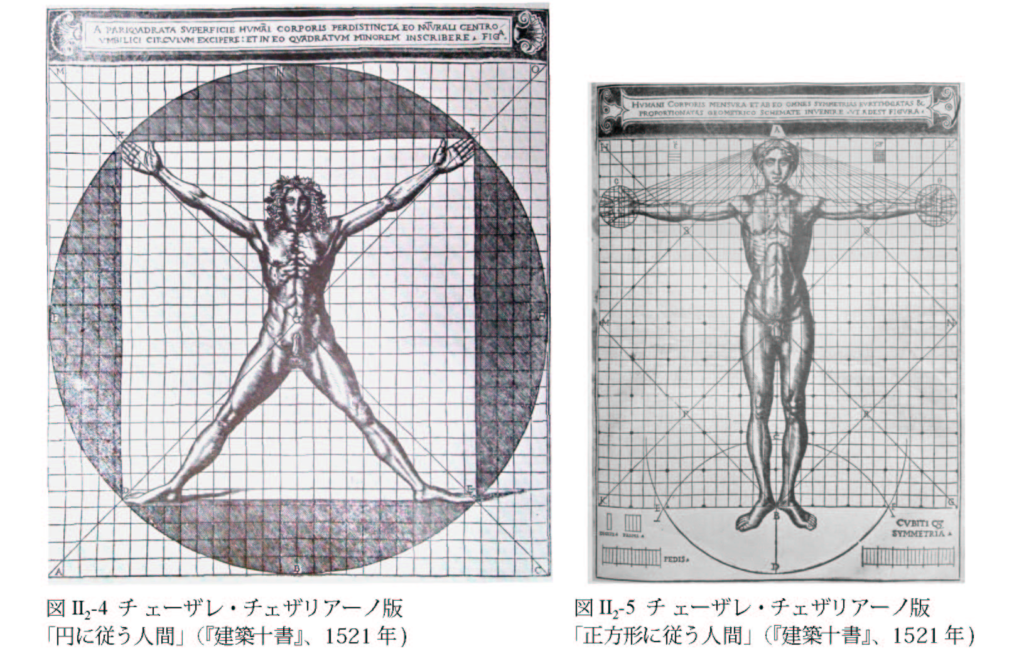
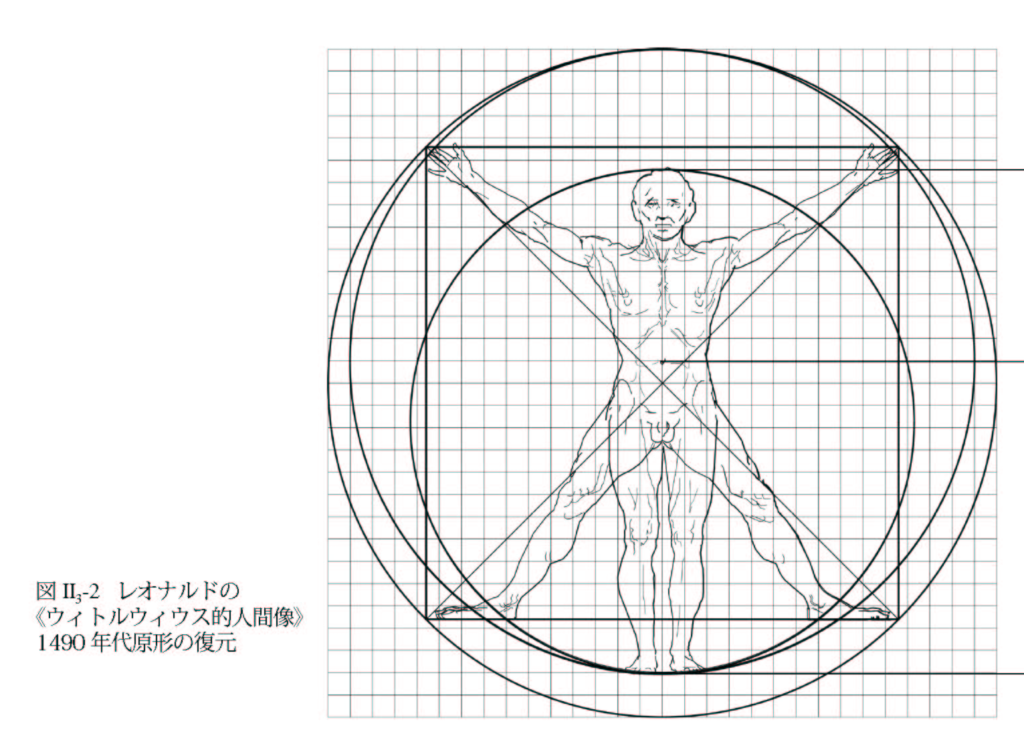
図 Ⅱ3-2 は前掲の図 Ⅱ3-1を踏まえて、作図したレオナルドの《ウィトルウィウス的人体像》の1490年代の原形として向川博士の考える復元であり、レオナルドの思考過程を類推することができる。へそ位置が身長を黄金分割しており、正方形の四隅に手先、足先が届いている。
図Ⅱ2-5の正方形に従う人間では、向川博士は底辺の弧の切片の長さを調べた。これは図中央の45度傾いた正方形の辺の長さの1/2を半径とする弧であって、その一方の中心は外枠の大きな正方形の底辺の中点から、図の中心線上に弧の半径の1/2の距離にある点である。もう一方の弧は底辺について他方と対称を為す。よって両者の交点、すなわち図Ⅱ2-5の点EとFは、外枠の正方形の底辺上に位置する。三角形CED、CDFは正三角形である。EFの長さは外枠正方形の辺の長さを単位とすると、(√2×√3)/4 と算出される。この値は、0.61237であって、黄金比 0.61803に対し極めて良い近似値である。向川博士はレオナルドがある時期この長さを黄金比として使っていたと推定している。
正五角形を描くにためには黄金比に相当する長さを得ねばならない。しかし、レオナルドのルネッサンス期では黄金比を用いて五角形を作図することは知られていなかった。前掲の図Ⅱ2-14に、図Ⅱ2-5の外枠の正方形の底辺に描かれた二つの弧と同じ形が描かれていて、レオナルドが正五角形を検討した様子が伺える。
向川博士は、1500年代半ばに成立した ウィトルウィウス 『建築十書』の中の 《ウィトルウィウス的人体像》 の大部分は、ホイヘンス稿本第七葉の円に内接する多角形を元にしたと考えている。さらに、1490年代にはレオナルドは《ウィトルウィウス的人間像》をチェザリアーノの「円に従う人間」と「正方形に従う人間」でのようにそれぞれ別の図像に表現したと推定している。
従来レオナルドの《人体権衡図》はウィトルウィウスの基準を音楽的調和比例によって基づいて示したものと解釈されてきた。レオナルドの《人体権衡図》の「正方形」と「円」を幾何学的な規制図形として捉えた研究は、向川博士のそれと1998年のクラウス・イーレとクラウス・シュレーアの共同研究以外には無かった。
「正方形」と「円」が幾何学的な意味を持ち、ウィトルウィウスの基準に含まれる黄金分割や黄金比の等比数列が明らかになった以上、《人体権衡図》を代表とする人体比例理論はその年代的なことを含めて、レオナルドの数学的知見を基に再検討が為されねばならない。
