Chapter 1 Leonardo’s Theory of Painting and its Proportional Theory
Introduction
There was Leonardo’s painting theory that influenced the Baroque painters Poussin, the Carracci brothers, and even Goethe.
The “Codex Urubino Latinus” is contained in the Vatican’s Library, which is widely accepted as a work of Leonard’s disciple Francesco Melzi in his later years to faithfully reproduce Leonardo’s intentions. In general, Leonardo’s “Theory of Painting” refers to the modern translation of this book.
On the other hand, there used to be something called “Sforza’s theory of painting”, which was written during the period of Leonaro’s residence in Milan and is now lost, and it is considered that there used to be “paragone” (comparative theory of arts) as an introduction among them. Luca Pacioli, a mathematician whom Leonardo became acquainted with in Milan, reported that Leonardo wrote “a book on the painting and the movement of the human body” through hard work, in the dedication of “De Divina Proportione ” dedicated to the Duke of Milan.
Lomazzo wrote that in “paragone” Leonardo discussed that which was higher paintings or sculptures. Leonardo stated in his “Theory of paintings” that “things that cannot withstand mathematical lighting cannot be called true academic discipline”, and the essential conditions are “must be based on experience” and “must be accompanied by quantitative proof ”.
However, Leonard’s mathematical findings have not been fully investigated. The problem was what the commandment in Windsor folio (Windsor 19118r), “Do not let non-mathematicians read my principles.”
There is also a document called “Codex Huygens” (Piermont Morgan’s Library in New York), in which there are many those seem to have ever been transcribed from the existing Leonard’s manuscript, and by many researchers, studies have been conducted on the relationship with Leonardo’s original manuscripts and about the writers who transcribed from them.
Erwin Panovsky published the results of his “Codex Huygens” in 1940. This was the first work to explain Leonardo’s painting theory.
Section 1 Leonardo da Vinci’s proportional theory
Dr. Mukaigawa clarified the basics of human body depiction from the results of Leonardo’s study of painting theory.
The rationale is the “Codex Huygens” (Codex Huygens MA1139). The first study of this manuscript was published by Panovsky in 1940, and Dr. Mukaigawa took it a step further.
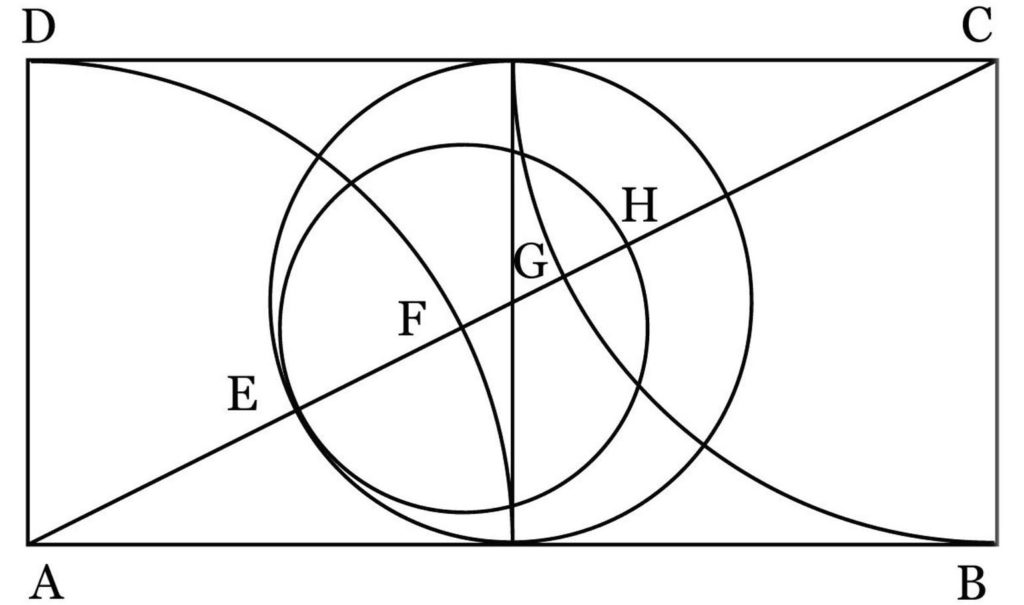
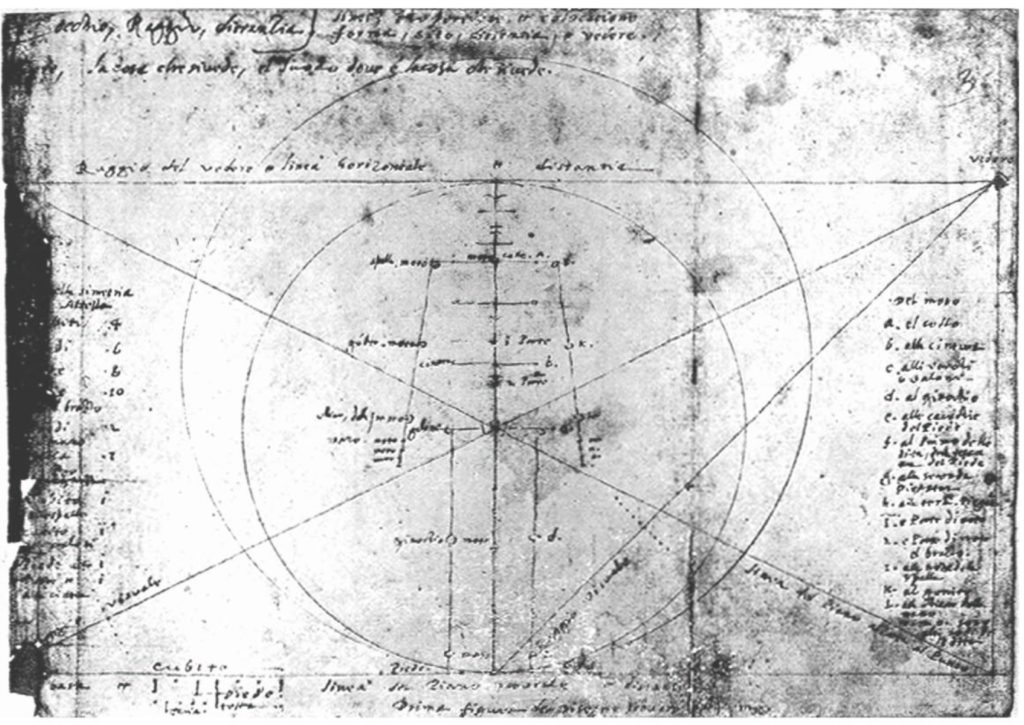
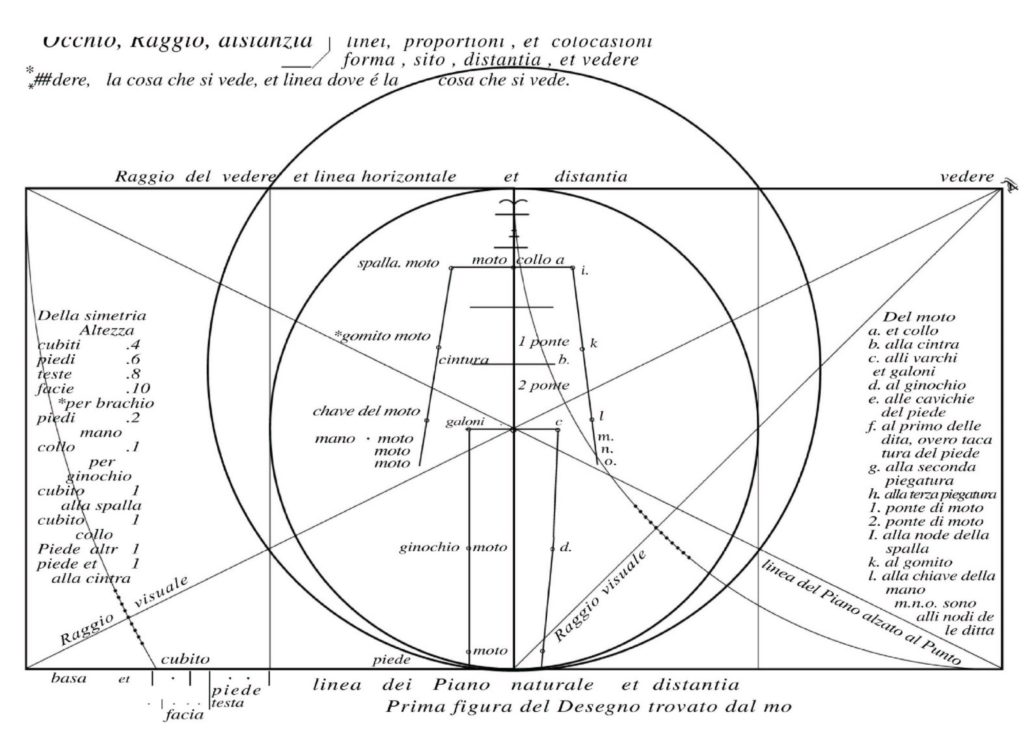
Figure I(1)-6 is the first folio of the Codex Huygens, and reference figure I(1)-6 is a reprint of it. (Since the figure numbers are the same as Dr. Mukaigawa’s original paper (self-published, in Japanese), those in this site are not in numerical order).
The diameter of a small circle is the height of the human body to be drawn, and a square with the diameter of this small circle as the left and right sides is drawn, and from these, a rectangle with a ratio of 1 to 2 is formed. The big circle is drawn so that it touches the lower side of the rectangle, centered on the point that divides the vertical centerline of the square by the golden ratio.
What must be emphasised here is the fact that the position of the navel in the expression of the human body divides the height into golden ratio since the days of ancient Greek sculpture. This became widespread in the mid-19th century, as described by German aesthetician Zeising. It was already known in the time of Leonardo, and Leonardo followed this fact. Two arcs with the short side of the rectangle (one side of the square) and the long side as the radius are drawn from the eye-shaped mark on the upper right of the rectangle, and the intersections with the diagonal line of the square and with the diagonal line of the rectangle are dotted lines. The human body encircled by a “small circle” is shown as a simple straight line, and the proportional reference line for each part of the body is shown as a horizontal line.
Panofsky called the “big circle” as the “circle” of Vitruvian man, and the body represented by a simple line opens both legs 60 degrees, extends the arms, and raises the arms 30 degrees above the horizontal centering at the shoulders. When the eagle posture is taken with wings spread, the fingertips come into contact with this “big circle”.
The center of the big circle is the navel position, which is the point that divides the height by the golden ratio, and the radius of the great circle is 0.6180 …… (= φ) when one side of the square is “1”.
In addition, many detailed explanations are written on this folio, and it is very difficult to decipher the written text because of ages and damage of the paper leaf, and it is difficult to see the intention of the painting. Leonardo’s manuscript is basically a memo, and we are the same, it is not a thing to show or leave for explanation to others but a reminder. It has a characteristics that reminds him of what he was thinking about.
In particular, the reference values for human body proportion, which are written in nineteen lines on the left side of the paper sheet, are shown by the symmetrical scale of “fractional method”, which indicates how many lengths of each part can be taken relatively in the height.
Section 2 Golden Ratio and Phiogenesis of Double Square
Dr. Mukaikawa found in this “Codex Huygens” the geometrical method of applying the golden ratio when Leonardo painted the “Vitruvian Man”, and named it “phiogenesis of double square”. Its mathematical description is given at the end of this section, but the main points are as follows.
The line segments having golden ratio 1: φ (= 0.6180 ……) are formed on a diagonal line of a rectangle with a side ratio of 1: 2. That is, in the inset 4,
GC: FG: EF: AE = 1: φ: φφ: φφφ. It means that the geometric series of the golden ratio is formed in sequence on the diagonal line.
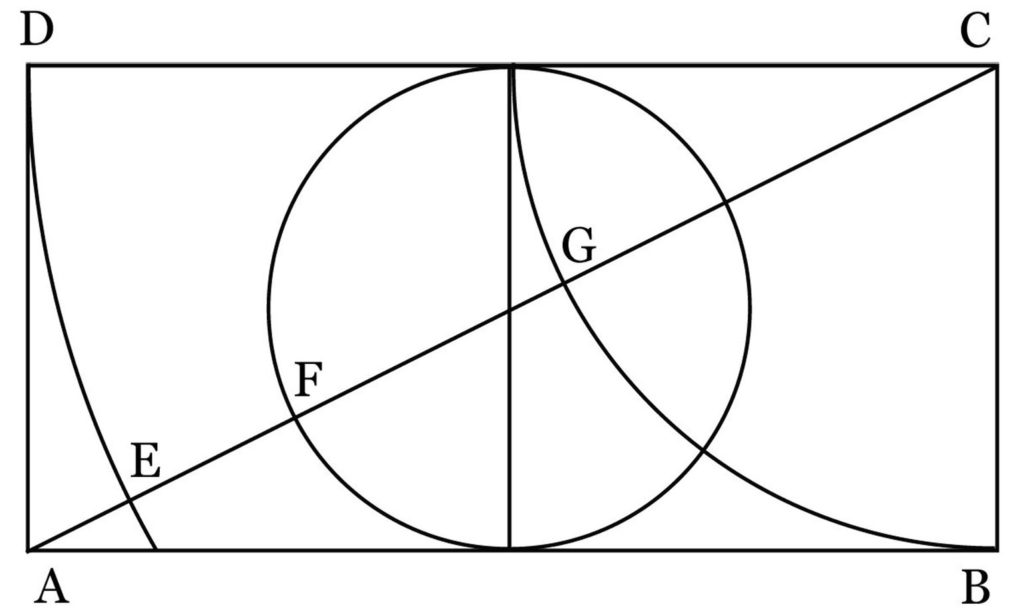
If you prepare a rectangle and line segments that form the geometrical series of the golden ratio above-mentioned on the painting screen, you can easily draw a line segment of this ratio. Leonard discovered this geometrical truth and introduced a strict measure of the golden ratio into his painting composition.
When constructing the screen, the painter can use this “phiogenesis of double square” to zoom in and out at the golden ratio of a particular line segment.
Leonardo used this principle to determine the length of each part of the human body and the positions of the eyes, nose and mouth.
Mona Lisa’s face is exactly the same as Leonardo’s face in their eyes, nose, and mouth, and it is said that the image in the painting is like a reflection of Leonardo’s own face. It is a natural consequence of being decided by this law.
Let’s return to the story of “big circle”. Panofsky called it the Vitruvian circle and encircled the figure with the arm raised. A circle corresponding to this is also drawn in Leonardo’s “Vitruvian Man” (refer to the first picture shown in the summary of Dr. Mukaigawa’s paper). However, the circle in this Leonardo’s case is different from the big circle in the Codex Huygens.
This difference will be explained later, but it seems that the circle of “Vitruvian Man” was drawn as if it surrounded the human body after painting the figure, but that is not the case. Leonardo painted his painting as a strictly mathematical consequence.
Leonardo discovered the principle, as presented in our present mathematical representation in the “Phiogenesis of double square” section shown below. Leonardo’s “painting theory” is not an armchair theory, but a combination of experience-based practicality and mathematical proof, and it was realized in the painting works on and after the Milan period.
At that time, symbols such as φ and π were not used, so irrational numbers were not treated as they are today. It is known that Leonardo’s encounter with Luca Patchouli, a mathematician from whom Leonardo learned the calculation of irrational numbers at the court of Milan, became a major turning point for the evolution of proportional theory.
Phiogenesis of Double Square
In the inset 4, the symbol O is attached to the center of the circle (center of the rectangle), and in the rectangle ABCD on the diagonal line AC, the intersection point G with a circle with a radius of unit length 1, the intersection F with a circle of a diameter of 1 and E with a circle of a radius 2.
Since φ = (√5−1) / 2 is the solution of
XX + X -1 = 0
Then
φφ = 1-φ
GC = 1 FG = FO + (OC-GC) = 1/2 + (√5 / 2-1) = (√5-1) / 2 = φ
AE = √5-2
EF = AO-AE-FO = √5 / 2- (√5-2) -1/2 = (3-√5) / 2 = 1- (√5-1) / 2 = 1-φ = φφ
AE = √5-2 = 2 × ((√5-1) / 2) - 1 = 2φ-1 = φ-φφ = φ (1-φ) = φ × φφ = φφφ
Therefore, GC : FG : EF : AE = 1 : φ : φφ : φφφ
By the same logic, in the system of the inset 5,
AE : EF : FG : GH = 1 : φ : φφ : φφφ
is derived.