レオナルド・ダ・ヴィンチ
―― その絵画と比例理論に関する研究 ――
ダン・ブラウンの『ダ・ヴィンチ・コード』 が2003 年に出版されて、その作品に残された秘密に脚光が当てられている。ここでレオナルドの暗号とされたのは、古代ローマの建築家ウィトルウィウスの記述に基づいた音楽的調和比例の身体区分に隠された黄金分割を指している。筆者の研究はダン・ブラウンがレオナルドの暗号とした《ウィトルウィウス的人間像》の臍の位置が黄金比の等比数列になることを三十年前に発見したことから始まっている 筆者の研究はダン・ブラウンがレオナルドの暗号とした《ウィトルウィウス的人間像》の臍の位置が黄金比の等比数列になることを三十年前に発見したことから始まっている 。

レオナルドの黄金分割は『ダ・ヴィンチ・コード』出版以降人口に膾炙され誰も疑問にもつものはいないが、筆者が研究を始めた当時、レオナルドが比例に黄金分割を使ったとする見方はまったく存在せず、レオナルド自身の黄金分割自体が疑問視されていた。そのため、ホイヘンス 稿本第一葉から導かれる筆者の命題「ダブル・スクエアーのフィオゲネシス」をヴェネチアの《人体権衡図》の黄金比の等比数列の根拠とした。
パノフスキーはホイヘンス稿本第一葉を、幾何学的メソッドにより規定される人体の形態と構造を著したものとして、レオナルドの《人体権衡図》に結びつけている。第一章で、ホイヘンス稿本第一葉から幾何学的に筆者の命題「ダブル・スクエアのフィオゲネシス」が導かれるので、パノフスキーが見落とした破線が《人体権衡図》の黄金比の等比数列の4 つの項を導くものと定義して、この紙葉の「線、プロポーション、場合により/形、位置、距離および見え方。見えるものと、見えるものがどこにあるかを示した線の見え方」と書かれた記文から、これがレオナルドの失われた「スフォルツァ絵画論」のコピーと仮定して、「ホイヘンス稿本」のこの紙葉がレオナルドの作図システムの原理を示したものと捉えている。その一方で二行目の「形、位置、距離、および見え方。見えるものと、見えるものがどこにあるかを示した線の見え方」という文章から、このシステムをレオナルドの線遠近法についての記述としても捉えている。

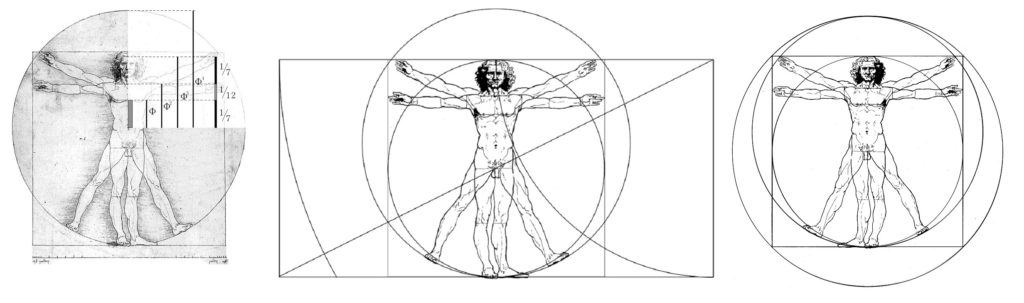
パノフスキーの「ホイヘンス稿本」の研究では見落されていたが、稿本第一葉から黄金比の等比数列が導かれる。レオナルドの《ウィトルウィウス的人間像》は、黄金分割の近似値および黄金分割や黄金比の等比数列に至るまで、時期によって異なる三つの形で扱われていた。黄金分割の近似値の概数で扱ったのがホイヘンス稿本第七葉で、黄金分割で扱われたものがオックスフォード紙葉であって黄金比の等比数列が適用されたものがヴェネチアの《人体権衡図》である。この内で、オックスフォード紙葉とホイヘンス稿本第一葉は、ウィトルウィウスの「円」と基準線の位置とが同じ扱いになっており、第一葉から黄金比の等比数列が導かれるので《人体権衡図》が最も高度なもので、従来《人体権衡図》の制作年代とされた1492年にはまだ黄金分割の作図ができないので、従来のヴェネチアの図の制作年代が誤ったものであることが判る。
パノフスキーは、ホイヘンス稿本第一葉を、幾何学的メソッドにより規定される人体の形態と構造を著したものとして《人体権衡図》に結びつけたが、問題はレオナルドの現存手稿にホイヘンス稿本第一葉の作図が残されていないことである。人体比例研究で見たように、従来レオナルドの《人体権衡図》の制作年代とされた年に描かれたのがホイヘンス稿本第七葉であるならば、《人体権衡図》の制作年代が問われなければならない。ホイヘンス稿本第一葉の図の上部に「線、プロポーション、場合により/形、位置、距離および見え方。見えるものと、見えるものがどこにあるのかを示した線の見え方」として、この図が人体比例だけでなく線遠近法の作図方法をも規定していることが判り、命題「ダブル・スクエアのフィオゲネシス」の系が《マギの礼拝》背系図の四本の対角線を導くものであることが判り、従来レオナルドの初期の作品とされた《マギの礼拝》の制作年代の下限が問題となる。
現存手稿には、ホイヘンス稿本第一葉が残されていないから、この図から導かれる黄金比の等比数列をレオナルドが見つけた時期が問われなければならず、レオナルドの線遠近法を《最後の晩餐》室内空間と《マギの礼拝》の板絵とを比較することで、ホイヘンス稿本第一葉の制作年代を再検討した。


本論文の構成は、人体比例、線遠近法共にレオナルドを代表する具体的作品を幾何学的に解析した後、レオナルド自身の記述とそれに関連した作品を対比している。《人体権衡図》研究を始めた当時、筆者の命題「ダブル・スクエアのフィオゲネシス」が《マギの礼拝》板絵の構図を反映することに気がついたが、「ホイヘンス稿本」をレオナルドの『絵画論』に結びつけたペドレッティや第七葉を1498 年以前の失われた意匠に結びつけたイルマ・リヒター女史などの定説では、《人体権衡図》と《マギの礼拝》の制作年代に齟齬が起きてくる。これはレオナルドの黄金分割を今日と同じ0.618…や1.618…として扱っているからである。
この問題を解決するために第三章ではレオナルド自身のリテラルな記述から黄金分割の問題を検討している。第四章以降で扱う線遠近法の準備として、アルベルティの『絵画論』で「誤った遠近法」の逓減率とされた《superbipartienti 》は、ルネッサンス前期から3 分の2 として使われた黄金分割であったことを示している。第四章では、十二使徒たちの習作を描いたアランデル手稿紙葉153r の表とマドリッド手稿II第四十八葉裏の表の《superbipartienti 》が対応しており、これが黄金分割として室内の作図に使われていたことが判る。このことからレオナルド自身の黄金分割も、誤った逓減率の3 分の2 から無理数のφ や黄金比の等比数列に至るまで時期によって扱い方が異なっていることが判る。
《最後の晩餐》室内の復元を通じて、レオナルドが線遠近法の作図に最初に黄金分割を当て嵌めたものが《マギの礼拝》背景図ではなくて、《最後の晩餐》だった。「正統作図法」で描いた当初の《最後の晩餐》にルカ・パチョーリとの邂逅から黄金分割の大きな値1.618…を掛けて奥行を拡大したのが現在の《最後の晩餐》である。第五章のウフィツィ美術館の《受胎告知》の解析から判ることは、額縁を含めた1 対2 の画面内部に距離点を設定したことで、同一画面に2 つの異なる舗床を併設したように、《最後の晩餐》では当初の格天井中央の桟が現行の格天井にそのまま拡大されている。「正統作図法」の場合、この桟の位置を合わせるのは大変だが「距離点法」の作図法を導入して簡潔にしていることである。これがそのまま距離点を移動した第六章の《マギの礼拝》背景図に活かされている。レオナルドの《マギの礼拝》背景図は、三十代の素描と考えられてきたが、《人体権衡図》と同様、1500 年代に入ってレオナルドがユークリッド幾何学に習熟してからの五十代半ばの素描と言える。

レオナルドの黄金分割や黄金比の数値は時期によって違い、 無理数φ を使うようになったのは数学者ルカ・パチョーリとの邂逅以降のことである。そして実際に彼が独力で無理数φ を用いるようになったのは、マドリッド手稿II の「等量学」やパリ手稿K2 紙葉26r のユークリッド『原論』第二巻命題11の外中比の作図から1504 年以降でなければ,使用できないことが判る。

筆者のレオナルド研究は、第一章で提示した幾何学的命題から導いた黄金比の等比数列を第二章から第七章までレオナルド作品に確認して、この原理がレオナルドの人体比例理論と線遠近法の作図システムに使われたことを証明している。そして、これが新しい見方として成立していることと、オックスフォード紙葉の代わりとして、1508 年頃にホイヘンス稿本第一葉から第六葉が新たに付け加えたものであっても、「ホイヘンス稿本」は失われた「スフォルツァ絵画論」のコピーとする見方が作品解析を通じて成立することが判るだろう。
第七章の《モナ・リザ》は、リザ・デル・ジョコンドの肖像画の他にレオナルドが完成した「スフォルツァ絵画論」の象徴として描かれたものであって、肖像の背景の風景を囲んだ円柱を入れて復元した場合、『絵画論』第二章の「画家の規範について」に書かれたグラティコラの編目格子の記述に合致していることが判る。
チェザリアーノ版「正方形に従う人間」足元のアーモンド形の切片は、4 分の √ 2 ×√ 3 、即ち極めて正確な近似値0.6123…になることを含めてレオナルドの円弧が《モナ・リザ》の人物の体の輪郭に使われていることから、ホイヘンス稿本第一葉の「大円」の前にレオナルドが「ウィトルウィウスの円」として使用していたのがこの円弧を基にしたものである。この正方形の底辺の切片はレオナルドの比例理論のパラダイムとして、「数学者ではないものに、私の原理を読ませてはならない」と語った根底には黄金分割が存在することを示している。
終章ではレオナルドの《人体権衡図》の制作年が1490 年代初めでなく、次のウィンザー紙葉19145r の書かれた日以降でなければ制作出来ない はずで「私は二つの曲線の辺をもつ角について、即ち角e の如き等しい彎曲度つまり同一の円から生じた等しい彎曲度をもつ角について、それを求積することを長い歳月をかけて求め続けてきたが、今1509 年5 月1 日の前夜,日曜日22 時,この課題を解いたのであった」という「シンメトリアの理法」に関する幾何学研究を絵画作品や「絵画学」など他の領域と結びつける試みは未開拓だったのではないだろうか。
レオナルドの《人体権衡図》を従来通り1492 年頃とすると、1509 年5 月1 日のウィンザー紙葉19145rとは20 年近い隔たりがあるが、《人体権衡図》の制作年代を1508 年から9 年前半とするとこの隔たりは無くなり、イーレとシュレーアの研究のウィンザー紙葉12280r のアルキメデスの「円」の面積も《人体権衡図》に結びつけられるから、「幾何学遊戯」が遊びではなくて幾何学的にウィトルウィウスの「シンメトリアの理法」が解けると確信していたことを示している。
向川博士の研究成果は次にまとめられる。
1.レオナルド・ダ・ヴィンチは幾何学を応用して絵の構図を決定していた。
2.向川氏はレオナルドが画構成に黄金比を適用した方法を見出し、「ダブルスクエアのフィオゲネシス」と名付けた。
3.向川氏はこれまで「ウィトルウィウス的人体図《人体権衡図》」「マギの礼拝」「最後の晩餐」について、レオナルドの絵画構成法を明らかにしてきた。
4.「ウィトルウィウス的人体図」において人体を囲む円の成り立ちを明らかにした。
5.絵画構成について、レオナルドは最初は黄金分割の近似値の概数、ついで黄金分割、更に「人体権衡図」では黄金比の等比数列を適用した。
6.ルーブル美術館蔵の「モナ・リザ」についてその理論を適用した。重要な要素はかって人物像の両側に描かれた柱であり、それを考慮すると、レオナルドの作図法が確認される。
7.レオナルドの複数の絵画の制作年代が従来の定説を覆されて、確定し得る。
